Математикийн үйлдлүүдэд нэг ба тэг тоонууд онцгой шинжүүдтэй. Үржих үйлдэлд нэг ба тэг
шинжтэй байдаг.
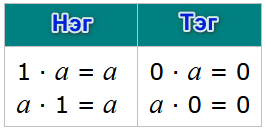
Үржих үйлдэлд нэгийн шинж
Нэгийг ямарч тоогоор үржүүлсэн үр дүн нь үржүүлсэн тоо өөрөө байна.
Жишээ. 1 · 3 = 1 + 1 + 1 = 3 гарна.
Ямарч тоог нэгээр үржүүлэхэд үр дүнд нь тухайн тоо өөрөө гардаг.
Жишээ. 4 · 1 = 4 байна. 4 ийг нэг л удаа авч нэмэх тул үр дүн 4 байна.
Дээрх жишээнүүдээс дурын a тооны хувьд
1 · a = a
a · 1 = a
тэнцэл үнэн гэсэн дүрэм гарч ирнэ. Дээрх тэнцлээс
Үржвэрийн аль нэгэн бүрдүүлэгч (үржиглхүүн эсхүл үржигч) нэгтэй тэнцүү байвал үржвэр нөгөө бүрдүүлэгчтэй тэнцүү
дүрмийг тодорхойлж болно.
Үржих үйлдэлд тэгийн шинж
Тэгийг ямарч тоогоор үржүүлсэн үр дүн нь тэг байна.
Жишээ. 0 · 3 = 0 + 0 + 0 = 0 гарна.
Ямарч тоог тэгээр үржүүлэхэд үр дүнд нь тэг гардаг.
Жишээ. 4 · 0 = 0 байна. 4 ийг нэг ч удаа авч нэмээгүй тул үр дүн тэг байна.
Дээрх жишээнүүдээс дурын a тооны хувьд
0 · a = 0
a · 0 = 0
тэнцэл үнэн гэсэн дүрэм гарч ирнэ. Дээрх тэнцлээс
Үржвэрийн аль нэгэн бүрдүүлэгч (үржиглхүүн эсхүл үржигч) тэгтэй тэнцүү байвал үржвэр тэгтэй тэнцүү
дүрмийг тодорхойлж болно.





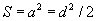
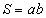
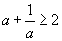 / энд a эерэг тоо / жишээн дээр авч үзье.
/ энд a эерэг тоо / жишээн дээр авч үзье. 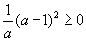 байна. Хаалтыг задалбал
байна. Хаалтыг задалбал 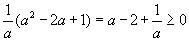 болох бөгөөд эндээс
болох бөгөөд эндээс 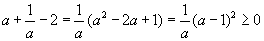 Эндээс a=1 үед л тэнцэл гарах нь харагдаж байна.
Эндээс a=1 үед л тэнцэл гарах нь харагдаж байна.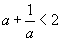 гэж үзье. Тэнцэл бишийн хоёр талыг a гаар үржүүлбэл a2 +1<2a буюу a2 +1−2a<0 өөрөөр (a−1)2 <0 болно. Энэ нь буруу тэнцэл биш тэгэхээр эсрэг тохиолдол нь үнэн болно.
гэж үзье. Тэнцэл бишийн хоёр талыг a гаар үржүүлбэл a2 +1<2a буюу a2 +1−2a<0 өөрөөр (a−1)2 <0 болно. Энэ нь буруу тэнцэл биш тэгэхээр эсрэг тохиолдол нь үнэн болно.
 функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол. тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.