Тэмдэглэгээ:
V - эзэлхүүн ; S - суурийн талбай ; 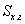 - хажуу гадаргуун талбай; P - бүтэн гадаргуу; h - өндөр; a, b, c - тэгш өнцөгт паралелпепидын хэмжээсүүд; A - зөв ба зөв зүсэгдсэн пирамидийн апофем; L - конусын бүрдүүлэгч; p - периметр эсвэл суурийн тойргийн урт; r - суурийн радиус; d - суурийн диаметр; R - шаарын радиус; D - шаарын диаметр; 1 ба 2 индексүүд нь зүсэгдсэн призм ба пирамидийн радиус, диаметр, периметр, дээд доод сууриудтай холбоотой.
- хажуу гадаргуун талбай; P - бүтэн гадаргуу; h - өндөр; a, b, c - тэгш өнцөгт паралелпепидын хэмжээсүүд; A - зөв ба зөв зүсэгдсэн пирамидийн апофем; L - конусын бүрдүүлэгч; p - периметр эсвэл суурийн тойргийн урт; r - суурийн радиус; d - суурийн диаметр; R - шаарын радиус; D - шаарын диаметр; 1 ба 2 индексүүд нь зүсэгдсэн призм ба пирамидийн радиус, диаметр, периметр, дээд доод сууриудтай холбоотой.
Призм / шулуун ба налуу / ба паралелпепид
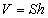
Шулуун призм
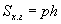
Тэгш өнцөгт паралелпепид
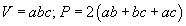
Куб
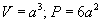
Пирамид / зөв ба зөв биш /
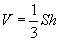
Зөв пирамид
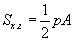
Зүсэгдсэн пирамид / зөв ба зөв биш /
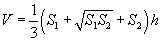
Зөв зүсэгдсэн пирамид
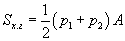
Бөөрөнхий цилиндр / шулуун ба налуу /
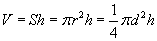
Бөөрөнхий цилиндр
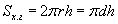
Бөөрөнхий конус / бөөрөнхий ба налуу /
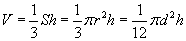
Бөөрөнхий конус
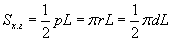
Зүсэгдсэн бөөрөнхий конус / бөөрөнхий ба налуу /
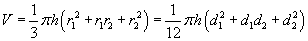
Зүсэгдсэн бөөрөнхий конус
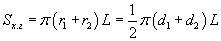
Шаар
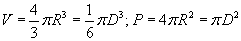
Хагас шаар
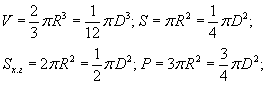
Шаарын сегмент
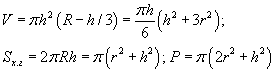
Шаарын үе
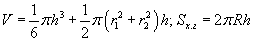
Шаарын сектор
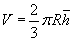
энд 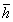 - секторт байгаа сегментийн өндөр
- секторт байгаа сегментийн өндөр





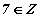 бичлэгийг "5 нь Z олонлогт харьяалагдана" эсхүл "5 нь Z олонлогийн элемент" гэж уншина.
бичлэгийг "5 нь Z олонлогт харьяалагдана" эсхүл "5 нь Z олонлогийн элемент" гэж уншина.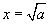 болно.
болно.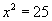 тэгшитгэл нь 5, -5 гэсэн хоёр шийдтэй. Шийдийг дараах хэлбэрээр
тэгшитгэл нь 5, -5 гэсэн хоёр шийдтэй. Шийдийг дараах хэлбэрээр 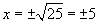 гэж бичдэг.
гэж бичдэг.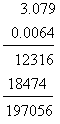
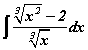 интеграл бод
интеграл бод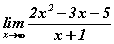 хязгаарыг бод.
хязгаарыг бод.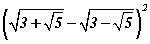 утгыг ол.
утгыг ол.