Энэ хичээлээр логарифм тэгшитгэлүүдийг бодох аргуудын талаар авч үзнэ. Хувьсагч утга нь логарифмын тэмдэгт байрлах тэгшитгэлийг логарифм тэгшитгэл гэдэг. Жишээ нь 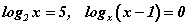
Логарифмын үндсэн адитгал, чанаруудын талаар Логарифм хичээлээс үзээрэй. Үүнээс гадна логарифм тэгшитгэлүүдийг бодож сурахад Үндсэн томьёонуудыг мэддэг байх хэрэгтэй. Логарифм тэгшитгэлийг бодох үндсэн дүрэм бол
- Логарифмын суурь тэгээс их ба нэгтэй тэнцүү биш байх ёстой
- Логарифм доорх илэрхийлэл тэгээс их байх ёстой. Өөрөөр хэлбэл эерэг байна.
- Тэгшитгэлийн шийд логарифмын тодорхойлогдох мужид харьяалагдаж байх ёстой
гэдгийг байнга санах явдал юм. За ингээд логарифм тэгшитгэлүүдийг бодох аргуудтай танилцая.
Нэг. Логарифмын тодорхойлолтоор бодогдох тэгшитгэлүүд
Ийм төрлийн тэгшитгэлүүд 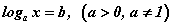 ерөнхий хэлбэртэй байна. Жишээ нь
ерөнхий хэлбэртэй байна. Жишээ нь
Бодлого 7.051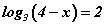 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Хоёр. Үндсэн чанаруудыг ашиглан бодогдох тэгшитгэлүүд
Логарифмын үндсэн чанаруудад
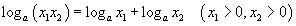 Үржвэрийн логарифм тэдгээрийн логарифмын нийлбэртэй тэнцүү
Үржвэрийн логарифм тэдгээрийн логарифмын нийлбэртэй тэнцүү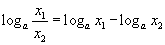 Ноогдворын логарифм хүртвэрийн болон хуваарийн логарифмын ялгавартай тэнцүү
Ноогдворын логарифм хүртвэрийн болон хуваарийн логарифмын ялгавартай тэнцүү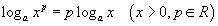 Логарифм доторх илэрхийлэлийн зэргийг логарифмын тэмдгээс гаргах ба оруулж болно.
Логарифм доторх илэрхийлэлийн зэргийг логарифмын тэмдгээс гаргах ба оруулж болно.
Эдгээр чанарыг тэгшитгэл бодоход өргөн ашигладаг тул цээжээр мэдэж байх хэрэгтэй. Жишээ авч үзье.
Бодлого 7.052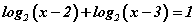 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Гурав. Логарифмыг хасах
Арга нь ижил суурьтай логарифм доорх тоонууд тэнцүү байна гэсэн чанар дээр үндэслэнэ. Эндээс тэгшитгэлийн тэнцүүгийн тэмдгийн хоёр талд ижил суурьтай логарифм байвал тэдгээрийн доорх илэрхийллүүдийг тэнцүүлэн бодно. Ингэхдээ тэгшитгэлийг бодох дүрмээ санаж байх хэрэгтэй.
Бодлого 7.053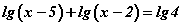 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Дөрөв. Орлуулах арга.
Тэгшитгэлүүдийг бодоход өргөнөөр ашигладаг универсаль арга. Аргыг хэрэглэх тохиолдлуудыг жишээн дээр авч үзье.
Бодлого 7.054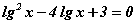 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Аргыг хэрэглэхийн өмнө анхдагч тэгшитгэлд логарифмын чанар, тохирох томьёонуудыг ашиглан урьдчилан зохих хувиргалтыг хийх шаардлага гарч болно. Жишээ нь
Бодлого 7.055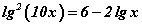 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Бодлого 7.056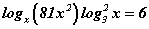 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Тав. Ижил суурьт шилжүүлэн бодох
Энэ арга нь 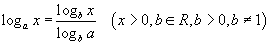 томьёог ашиглан тэгшитгэлийн гишүүдийг ижил суурьт шилжүүлэн бодох юм. Олон тооны тэгшитгэлийг энэ томьёог ашиглан ижил суурьт шилжүүлээд цаашид бидний үзсэн аргуудыг ашиглан боддог тул томьёог цээжлэх хэрэгтэй.
томьёог ашиглан тэгшитгэлийн гишүүдийг ижил суурьт шилжүүлэн бодох юм. Олон тооны тэгшитгэлийг энэ томьёог ашиглан ижил суурьт шилжүүлээд цаашид бидний үзсэн аргуудыг ашиглан боддог тул томьёог цээжлэх хэрэгтэй.
Бодлого 7.057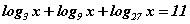 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Зургаа. Логарифмчлах арга.
Суурь болон зэрэг илтгэгчид үл мэдэгдэгч агуулагдсан тэгшитгэлийг бодохдоо логарифмчлах аргыг ашигладаг. Хэрвээ зэрэг илтгэгчид логарифм байвал тэгшитгэлийн хоёр талыг зэрэгт байгаа логарифмын сууриар логарифмчилна. Жишээ авч үзье.
Бодлого 7.058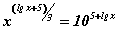 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Долоо. Тусгай томьёог ашиглах арга.
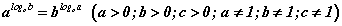 гэсэн томьёо байдаг. Өөрөөр хэлбэл аливаа тооны зэрэгт байгаа логарифм доорх тоо болон суурийг солин бичиж болно гэсэн үг. Энэ томьёо сурах бичгүүдэд нэг их тааралдаад байдаггүй тул шууд цээжлээд аваарай.
гэсэн томьёо байдаг. Өөрөөр хэлбэл аливаа тооны зэрэгт байгаа логарифм доорх тоо болон суурийг солин бичиж болно гэсэн үг. Энэ томьёо сурах бичгүүдэд нэг их тааралдаад байдаггүй тул шууд цээжлээд аваарай.
Бодлого 7.059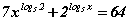 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Найм. Хоёрдугаар эрэмбийн нэг төрлийн тэгшитгэлийг бодох
Ийм төрлийн тэгшитгэлийг бодохдоо аль нэг 2-р эрэмбийн гишүүнд тэгшитгэлийн бүх гишүүдийг хуваагаад дараа нь шинээр хувьсагч оруулан квадрат тэгшитгэл болгон боддог. Квадрат тэгшитгэлээ бодоод шийдийг орлуулгадаа буцаан тавих замаар анхны тэгшитгэлийн шийдийг олно.
Бодлого 7.060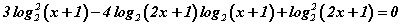 тэгшитгэлийг бод.
тэгшитгэлийг бод.





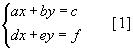 хэлбэрийн тэгшитгэлийн системийг
хэлбэрийн тэгшитгэлийн системийг 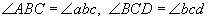 гэх мэт байна.
гэх мэт байна.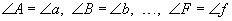 , харин талууд нь порпорционал байна.
, харин талууд нь порпорционал байна.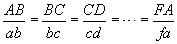
 илэрхийллийг хялбарчил.
илэрхийллийг хялбарчил.
 задаргааны 6-р гишүүнийг ол.
задаргааны 6-р гишүүнийг ол.