Энэхүү хичээлээр бид квадрат тэгшитгэлтэй холбогдолтой шийдийг олох томьёо, Виетийн терем, квадрат гурван гишүүнтийг үржвэрт задлах талаар авч үзэх болно. 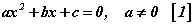 хэлбэрийн тэгшитгэлийг квадрат тэгшитгэл гэдэг. a, b тоонуудыг үл мэдэгдэгчийн коэффициентүүд харин c -г сул гишүүн гэдэг. a≠0 байх
хэлбэрийн тэгшитгэлийг квадрат тэгшитгэл гэдэг. a, b тоонуудыг үл мэдэгдэгчийн коэффициентүүд харин c -г сул гишүүн гэдэг. a≠0 байх 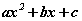 илэрхийллийг квадрат гурван гишүүнт гэнэ.
илэрхийллийг квадрат гурван гишүүнт гэнэ.
Бүрэн бус квадрат тэгшитгэл
Хэрвээ [1] квадрат тэгшитгэлийн b эсхүл c нь тэгтэй бол түүнийг бүрэн бус квадрат тэгшитгэл гэдэг. Ийм төрлийн тэгшитгэлийг бодох нь их амар энгийн байдаг. Жишээ авч үзье.
Бодлого. 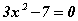 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Бодолт.
Тэгшитгэлийн тэнцүүгийн тэмдгийн хоёр талд үл мэдэгдэгч сул гишүүдийг гаргавал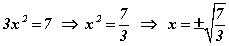
Бодлого. 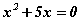 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Бодолт.
x -ийг хаалтны өмнө гаргавал 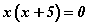 хэлбэртэй болох бөгөөд үржвэр тэгтэй тэнцүү байхын тулд үржигдхүүнүүдийн нэг нь тэгтэй тэнцүү нөхцлийн дагуу
хэлбэртэй болох бөгөөд үржвэр тэгтэй тэнцүү байхын тулд үржигдхүүнүүдийн нэг нь тэгтэй тэнцүү нөхцлийн дагуу 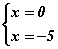 байна. Энэ нь манай тэгшитгэлийн шийдүүд болно.
байна. Энэ нь манай тэгшитгэлийн шийдүүд болно.
Бүтэн квадрат ялгах
Шийдийг олох томьёог санахгүй байсан ч ямар ч квадрат тэгшитгэлийг бодох боломжтой. Үүний тулд бүтэн квадрат ялгах хэрэгтэй. Энэ аргыг илэрхийлэл хураангуйлах, хувиргалт хийхэд маш өргөнөөр ашигладаг. Жишээ авч үзье.
Бодлого. 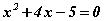 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Бодолт.
Тэгшитгэлийн хоёр талд 9-ийг нэмэн өгье. 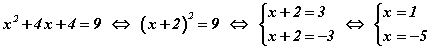
Бодлого. 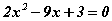 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Бодолт.
Бид шийдийн томьёо ашиглахгүй бодох гэж байгаа болохоор квадрат гурван гишүүнтээс бүтэн квадрат ялгах хэрэгтэй. Үүний тулд хоёр талыг 2-оор үржүүлээд нэмэлт оруулан өгвөл
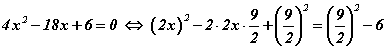 болно. Шууд томьёо ялгаад нэмсэн /хассан ч байж болно/ зүйлээ тэнцүүгийн тэмдгийн нөгөө талд нэмэн өгч байгааг сайн анзаараарай. Одоо бид бүтэн квадрат ялгах боломжтой болсон тул цааш бодоход хүндрэлгүй.
болно. Шууд томьёо ялгаад нэмсэн /хассан ч байж болно/ зүйлээ тэнцүүгийн тэмдгийн нөгөө талд нэмэн өгч байгааг сайн анзаараарай. Одоо бид бүтэн квадрат ялгах боломжтой болсон тул цааш бодоход хүндрэлгүй.
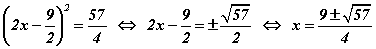
Бодлого. 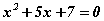 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Бодолт.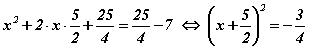 болох тул тэгшитгэл шийдгүй.
болох тул тэгшитгэл шийдгүй.
Санамж:
Ийм аргаар тэгшитгэлийг бодохдоо квадрат гурван гишүүнтээс бүтэн квадрат ялгахад юу дутаж байгааг олон харахад л хангалттай.
Квадрат тэгшитгэлийн шийдийг олох томьёо
Бүтэн квадрат ялгах аргыг квадрат тэгшитгэлийн ерөнхий тохиолдол [1] -д хэрэглэж болно. Ингэснээр та бидний сайн мэдэх квадрат тэгшитгэлийн шийдийн томьёог гарган авна. Бидэнд 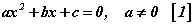 байлаа гэж үзээд хоёр талыг нь a -гаар үржүүлье. Тэгвэл
байлаа гэж үзээд хоёр талыг нь a -гаар үржүүлье. Тэгвэл
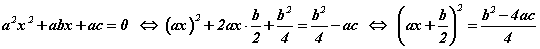 болно.
болно.
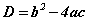 тоог [1] тэгшитгэлийн дискриминант гэнэ. Дискриминантын утгаас хамааран доорх тохиолдлууд гарч ирдэг.
тоог [1] тэгшитгэлийн дискриминант гэнэ. Дискриминантын утгаас хамааран доорх тохиолдлууд гарч ирдэг.
- D<0 бол [1] тэгшитгэл шийдгүй.
- D=0 бол [1] тэгшитгэл цорын ганц шийдтэй.
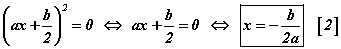
- D>0 бол [1] тэгшитгэл хоёр өөр шийдтэй.
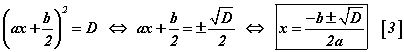
[3] -томьёо нь [1] тэгшитгэлийн шийдийн томьёо бөгөөд харин [2] -томьёо нь D=0 байх үеийн тухайн тохиолдол болно.
Бодлого. 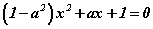 тэгшитгэлийг цорын ганц шийдтэй байлгах a -гийн хэдэн утга байгааг тодорхойл.
тэгшитгэлийг цорын ганц шийдтэй байлгах a -гийн хэдэн утга байгааг тодорхойл.
Бодолт.
Энэхүү энгийн бодлогод нэг жижигхэн асуудал байгаа. a=±1 гэсэн утгыг тусд нь авч үзэхийг мартаж болохгүй. Эдгээр утганд тэгшитгэл квадрат биш шугаман болон хувирна. a=1 үед тэгшитгэл x+1=0 болсноор x=-1 харин a=-1 үед тэгшитгэл x=1 гэсэн цорын ганц шийдүүдтэй. Харин a≠±1 үед өгөгдсөн тэгшитгэл квадрат болох бөгөөд дискриминант нь 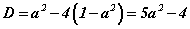 байна. Цорын ганц шийдтэй байх тохиолдол бол D=0 байх ёстой. Өөрөөр хэлбэл
байна. Цорын ганц шийдтэй байх тохиолдол бол D=0 байх ёстой. Өөрөөр хэлбэл 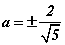 үед тэгшитгэл цорын ганц шийдтэй. Иймээс a -гийн 4 утганд тэгшитгэл цорын ганц шийдтэй болно.
үед тэгшитгэл цорын ганц шийдтэй. Иймээс a -гийн 4 утганд тэгшитгэл цорын ганц шийдтэй болно.
Хариу.
4
Бодлого.
a параметрийн ямар утганд 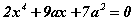 тэгшитгэл дор хаяхад нэг бүхэл шийдтэй байх вэ?
тэгшитгэл дор хаяхад нэг бүхэл шийдтэй байх вэ?
Бодолт.
Энд x, a -гийн үүргийг солих нь гол санаа юм. Өөрөөр хэлбэл x хувьсагчийг параметр харин a параметрийг хувьсагч болгох юм. Ингэвэл тэгшитгэл a гаас хамаарсан квадрат тэгшитгэл болох бөгөөд асуулт маань x параметрийн ямар бүхэл утганд 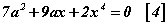 тэгшитгэл утгатай бөгөөд тэдгээрийг олох болон хувирах юм. Дискриминантыг тодорхойлбол
тэгшитгэл утгатай бөгөөд тэдгээрийг олох болон хувирах юм. Дискриминантыг тодорхойлбол 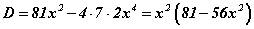 гарна. Эндээс зөвхөн x=0, x=-1, x=1 гэсэн гурван бүхэл утганд дискриминант эерэг гэдэг нь харагдаж байна. Эндээс
гарна. Эндээс зөвхөн x=0, x=-1, x=1 гэсэн гурван бүхэл утганд дискриминант эерэг гэдэг нь харагдаж байна. Эндээс
- x=0 үед [4] тэгшитгэлээс a=0 гарна.
- x=1 үед
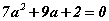 тэгшитгэлээс a=-1 ба a=-7/2 гарна.
тэгшитгэлээс a=-1 ба a=-7/2 гарна. - x=-1 үед
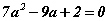 тэгшитгэлээс a=1 ба a=7/2 гарна.
тэгшитгэлээс a=1 ба a=7/2 гарна.
Хариу
0; ±1; ±7/2
b=2k байх үеийн шийдийн хураангуй томьёо
b=2k үед 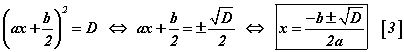 томьёоны ашигтай хувилбар бий болдог.
томьёоны ашигтай хувилбар бий болдог. 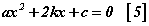 тэгшитгэлийг авч үзье. Түүний дискриминант
тэгшитгэлийг авч үзье. Түүний дискриминант 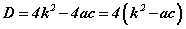 болох бөгөөд энэ тохиолдолд томьёо [3] нь
болох бөгөөд энэ тохиолдолд томьёо [3] нь 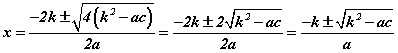 шилжинэ. Энэ бол [5] тэгшитгэлийн шийдийн томьёо юм.
шилжинэ. Энэ бол [5] тэгшитгэлийн шийдийн томьёо юм. 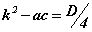 гэдгийг харгалзан үзвэл томьёог
гэдгийг харгалзан үзвэл томьёог
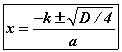 хэлбэрээр бичиж болно. Энэхүү томьёо нь шалгалтын үед таны үнэт цагийг хэмнэх учир түүнийг мэдэж байхыг зөвлөе. Жишээ авч үзье.
хэлбэрээр бичиж болно. Энэхүү томьёо нь шалгалтын үед таны үнэт цагийг хэмнэх учир түүнийг мэдэж байхыг зөвлөе. Жишээ авч үзье.
Бодлого. 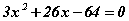 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Бодолт.
Тэгшитгэлийн хувьд k=13 тул 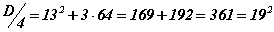 болно. Эндээс
болно. Эндээс
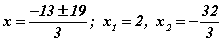 гарна. [3] томьёогоор тэгшитгэлийг бодох нь илүү төвөгтэй гэдгийг та туршаад үзээрэй.
гарна. [3] томьёогоор тэгшитгэлийг бодох нь илүү төвөгтэй гэдгийг та туршаад үзээрэй.
Виетийн теорем
Квадрат тэгшитгэлийн шийдүүд түүний коэффициентүүдтай энгийн харьцаагаар холбоотой байдаг.
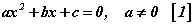 квадрат тэгшитгэл x1, x2 гэсэн шийдтэй гэж үзвэл (энд D=0 буюу x1=x2 тохиолдолч бас орно)
квадрат тэгшитгэл x1, x2 гэсэн шийдтэй гэж үзвэл (энд D=0 буюу x1=x2 тохиолдолч бас орно) 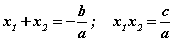 томьёо хүчинтэй. Энэхүү томьёог Виетийн теорем гэдэг. Теорем тэгшитгэлийн шийдийг олох
томьёо хүчинтэй. Энэхүү томьёог Виетийн теорем гэдэг. Теорем тэгшитгэлийн шийдийг олох 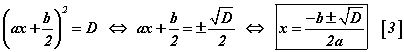 томьёонд шууд тооцоо хийх аргаар батлагдана. Тооцоо хийгээд үзвэл
томьёонд шууд тооцоо хийх аргаар батлагдана. Тооцоо хийгээд үзвэл 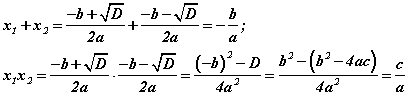 болно.
болно.
Виетийн теоремийг x1 , x2 шийдийн аль нэг нь [1] тэгшитгэлийн шийд биш бол теоремийн аль нэгэн тэгшитгэл биелэгдэхгүй гэж тодорхойлж бас болно. Энэ тодорхойлолтыг квадрат тэгшитгэлийн шийдийг олох томьёогоор гарган авсан шийдүүдийг шалгахад их хэрэгтэй. 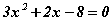 тэгшитгэлийг бодох хэрэгтэй боллоо гэе. Шийдийг олох хураангуй томьёог ашиглахад
тэгшитгэлийг бодох хэрэгтэй боллоо гэе. Шийдийг олох хураангуй томьёог ашиглахад
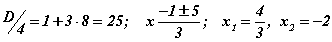 болно. Үүний дараа хэдхэн секунд зарцуулан шийдийг Виетийн томьёогоор шалгах хэрэгтэй. За шалгаад үзье.
болно. Үүний дараа хэдхэн секунд зарцуулан шийдийг Виетийн томьёогоор шалгах хэрэгтэй. За шалгаад үзье. 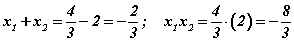 шийдүүд -b/a , c/a тай тэнцүү байгаа болохоор зөв гэсэн үг. Хэрвээ Виетийн аль нэгэн томьёо буруу хариу өгсөн бол тэгшитгэлийн шийдийг олох үедээ хаана нэгтээ алдаа гаргасан гэсэн үг. Иймд энэхүү дүрмийн хэрэглэж занших хэрэгтэй. Учир нь квадрат тэгшитгэл илүү нарийн тооцоолол бүхий бодлогын нэг хэсэг болох нь ихээр тохиолддог тул шийдийг олох явцдаа алдаа гаргавал цаашхи бүх үйлдлүүд алдаатай болно. Ийм үед Виетийн теорем нь хамгаалалтын хэрэгсэл болон өгнө. Гэхдээ Виетийн теоремыг тооцооллын алдааг шалгах хэрэгсэл гэж ойлгож болохгүй. Түүнийг ашиглах хүрээ үүнээс хамаагүй өргөн. Тухайлбал Виетийн теоремоор тэгшитгэлийн шийдийг олох боломжтой.
шийдүүд -b/a , c/a тай тэнцүү байгаа болохоор зөв гэсэн үг. Хэрвээ Виетийн аль нэгэн томьёо буруу хариу өгсөн бол тэгшитгэлийн шийдийг олох үедээ хаана нэгтээ алдаа гаргасан гэсэн үг. Иймд энэхүү дүрмийн хэрэглэж занших хэрэгтэй. Учир нь квадрат тэгшитгэл илүү нарийн тооцоолол бүхий бодлогын нэг хэсэг болох нь ихээр тохиолддог тул шийдийг олох явцдаа алдаа гаргавал цаашхи бүх үйлдлүүд алдаатай болно. Ийм үед Виетийн теорем нь хамгаалалтын хэрэгсэл болон өгнө. Гэхдээ Виетийн теоремыг тооцооллын алдааг шалгах хэрэгсэл гэж ойлгож болохгүй. Түүнийг ашиглах хүрээ үүнээс хамаагүй өргөн. Тухайлбал Виетийн теоремоор тэгшитгэлийн шийдийг олох боломжтой.
Виетийн урвуу теорем.
a, b, c, x1 , x2 тоонууд 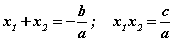 харьцаагаар холбогдож байвал x1 , x2 тоонууд
харьцаагаар холбогдож байвал x1 , x2 тоонууд 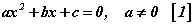 квадрат тэгшитгэлийн шийд болно. Жишээ авч үзье.
квадрат тэгшитгэлийн шийд болно. Жишээ авч үзье.
Бодлого. 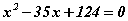 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Бодолт.
Нийлбэр нь 35, үржвэр нь 124 байх хоёр тоог олох гээд үзье. Эдгээр тоонууд бол 31 ба 4 юм. Виетийн урвуу теоремоор энэ тоонууд тэгшитгэлийн шийдүүд болно.
Бодлого. 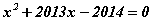 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Бодолт.
Тэгшитгэлийн шийдийг олох томьёогоор дискриминантыг тооцоход нилээд ажил болно. Энд тийм тооцоо хэрэггүй. x1=1 тэгшитгэлийн шийд гэдгийг амархан олно. Тэгвэл Виетийн теоремоор x2=-2014 гэдгийг тооцон олно.
Тэгшитгэл болгоныг Виетийн теоремоор бодоод байх боломжгүй. Зөвхөн дискриминантаас бүхэл язгуур гарах үед шийдийг сонгох боломжтой байдаг. Дискриминантаас иррационал тоо гарах үед шийд сонгох нь төвөгтэй бүр шийдгүй үед сонголт боломжгүй болно. Гэхдээ шалгалт дээр Виетийн теоремтой холбоотой нилээд төвөгтэй бодлогууд ихээр ирдэг. Хэдэн жишээ авч үзье.
Бодлого. 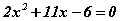 тэгшитгэлийн хувьд
тэгшитгэлийн хувьд 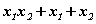 утгыг ол.
утгыг ол.
Бодлого
Хэрвээ x1, x2 нь 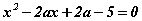 тэгшитгэлийн шийд бол a параметрийн ямар утганд
тэгшитгэлийн шийд бол a параметрийн ямар утганд 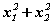 хамгийн бага утгатай байх вэ?
хамгийн бага утгатай байх вэ?
Бодлого
Хэрвээ x1, x2 нь 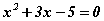 тэгшитгэлийн шийд бол
тэгшитгэлийн шийд бол 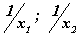 шийдтэй квадрат тэгшитгэл
шийдтэй квадрат тэгшитгэл 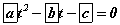 хэлбэртэй байх ба a, b, c -г ол.
хэлбэртэй байх ба a, b, c -г ол.
Бодлого
x1 , x2 , x3 , x4 тоонууд x1 < x2 < x3 < x4 дараалалтай бөгөөд 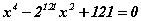 тэгшитгэлийн өөр өөр шийдүүд бол
тэгшитгэлийн өөр өөр шийдүүд бол 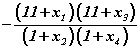 илэрхийллийн утгыг ол.
илэрхийллийн утгыг ол.
Квадрат гурван гишүүнтийг үржвэрт задлах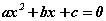 квадрат тэгшитгэлийн шийдүүдийг
квадрат тэгшитгэлийн шийдүүдийг 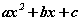 квадрат гурван гишүүнтийн шийд гэж бас нэрлэдэг. Квадрат гурван гишүүнтийн шийдийг мэдэж байвал түүнийг үржвэрт задалж болно. x1, x2 ийг
квадрат гурван гишүүнтийн шийд гэж бас нэрлэдэг. Квадрат гурван гишүүнтийн шийдийг мэдэж байвал түүнийг үржвэрт задалж болно. x1, x2 ийг 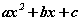 гурван гишүүнтийн шийдүүд гэвэл
гурван гишүүнтийн шийдүүд гэвэл 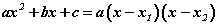 тэнцэл хүчинтэй байна.
тэнцэл хүчинтэй байна.
Тэнцлийг баталъя. Үүний тулд тэнцлийн баруун талын хаалтыг задлаад Виетийн теоремийг хэрэглэвэл 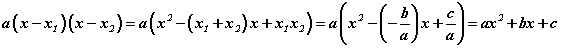 тэнцэл гарснаар батлагдлаа.
тэнцэл гарснаар батлагдлаа.
Бодлого. 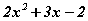 квадрат гурван гишүүнтийг үржвэрт задал.
квадрат гурван гишүүнтийг үржвэрт задал.
Бодолт.
Гурван гишүүнтийг квадрат тэгшитгэл болгон бодвол 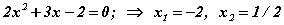 байна. Одоо гурван гишүүнтийг үржвэрт задлах томьёоны дагуу
байна. Одоо гурван гишүүнтийг үржвэрт задлах томьёоны дагуу 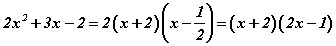 болно.
болно.





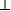 AB ба AO = OB гэе
AB ба AO = OB гэе
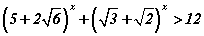 тэнцэтгэл бишийг бод.
тэнцэтгэл бишийг бод.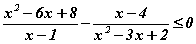 тэнцэтгэл бишийг бод.
тэнцэтгэл бишийг бод.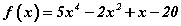 функцийн уламжлалыг олоорой.
функцийн уламжлалыг олоорой.