Шүргэгчийн тэгшитгэл

Энэ хичээлээр шүргэгч тэгшитгэлийг олох бодлогуудын талаар авч үзэцгээе. Ямар нэгэн функцийн график татсан шүргэгч шулууны тэгшитгэлийг олох, шүргэлтийн цэгийг олох гэх мэтээр шүргэгч шулуунтай холбоотой бодлогууд ЭЕШ -нд ирдэг. Шүргэгч шулууны тэгшитгэлийг гаргахын тулд уламжлалын геометр утгыг санацгаая. Хэрвээ y=f(x) функцийн графикийн x0 цэгт шүргэгч татвал түүний налуун коэффициент нь шүргэгч болон OX тэнхлэгийн эерэг чиглэл хоёрын хоорондох өнцгийн тангенстай тэнцүү байдаг.

Уламжлалын геометр утгаар x0 цэг дээрх функцийн уламжлалын утга нь энэхүү налуун коэффициенттой тэнцүү байдгийг бид мэднэ.

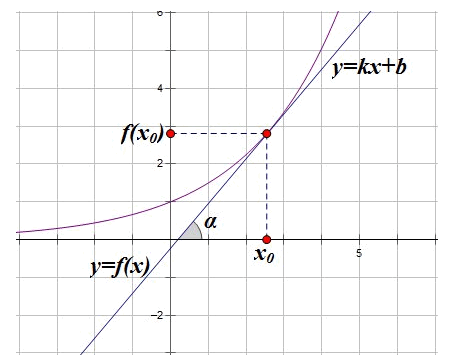
Дээрх тодорхойлолтыг томьёогоор илэрхийлбэл 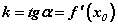. Функцийн графикт шүргэгчийн тэгшитгэлийг гаргахын тулд шүргэгч дээр (x,y) координат бүхий дурын цэгийг авъя.

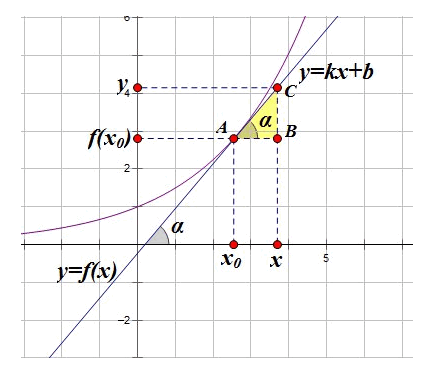
ABC гурвалжинг авч үзвэл тангенсын тодорхойлолтын дагуу 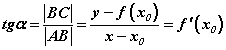гэдэг нь харагдана. Эндээс 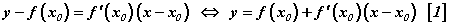гарна. Сүүлийн [1] тэгшитгэл бол y=f(x) функцийн графикийн x0 цэгт татсан шүргэгч шулууны тэгшитгэл юм. Тэгшитгэлийн гаргалтыг сайн үзээд [1] томьёог тогтоон аваарай. Томьёоны гаргалгаа их энгийн тул тайлбарлаад байх зүйлгүүй гэж бодож байна. Зөвхөн зургаа л сайн ойлговол бүх зүйл ойлгомжтой. Гаргалгааг үзүүлж байгаа нь математикийн томьёонууд хаа нэгэн газраас зүгээр гараад ирдэггүй бүгд зүй тогтолтой байдгийг харуулах гэсэн юм.
Тэгэхлээр шүргэгч шулууны тэгшитгэлийг бичихийн тулд бидэнд функцийн тэгшитгэл, шүргэгч дайран гарах цэгийг мэдэж байхад л хангалттай. Харин x0 цэг дээрх функцийн утга болон уламжлалын утгыг бид тооцон гаргаж чадна.  
Шүргэгчийн тэгшитгэлийг олох бодлогууд үндсэндээ 3 төрөлд хуваагдана.

1. Шүргэлтийн цэг x0 өгөгдсөн.

Бодлого 13.026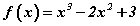
функцийн графикийн x=1 цэгт татсан шүргэгчийн тэгшитгэлийг бич.
Бодолт

Бодлого 13.027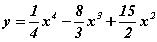
функцийн графикт OX тэнхлэгтэй паралел шүргэгчдийн шүргэлтийн цэгүүдийн абсциссыг ол.
Бодолт

2. Шүргэгчийн налуун коэффициент өгөгдсөн. Өөрөөр хэлбэл x0 цэг дээрх функцийн уламжлалын утга өгөгдсөн.

Бодлого 13.028
y=-x+3 шулуунтай паралел 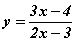функцийн графикт шүргэх шулууны тэгшитгэлийг бич.
Бодолт

3. Шүргэлтийн цэг биш боловч шүргэгч дайран өнгөрөх цэгийн координат өгөгдсөн.

Бодлого 13.029
A(3,1) цэгийг дайрах 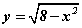функцийн графикийн шүргэгчийн тэгшитгэлийг ол.
Бодолт

Мэдээлэл таалагдсан бол найзуудтайгаа хуваалцаарай.

Холбоотой материалууд
Үржвэрийн шинжүүд

  Нээгдсэн тоо: 603 Нийтийн

Арифметикийн үйлдлүүдийн шинжүүдийг мэдэхгүй ч хүмүүс тэдгээрийг тооцоонд өргөн ашигладаг. Энэ удаа үржвэрийн шинжүүдийг аьч үзье.

Байр солих шинж.

Үржигдхүүнүүдийн байрыг солиход үржвэр өөрчлөлгдөхгүй. Өөрөөр хэлбэл үржвэрт орж буй гишүүдийн байрыг солиход үржвэрт нөлөөлөхгүй гэсэн үг. Эндээс дурын a, b тоонууд эсхүл илэрхийллийн хувьд a·b=b·a байна.

Жишээ

6·7=7·6 = 42
4·2·3=3·2·4 = 24
a·b·c=c·a·b=b·c·a

Нэг үл мэдэгдэгчтэй шугаман тэгшитгэл

  Нээгдсэн тоо: 6096 Нийтийн

ax+b=0 хэлбэрийн тэгшитгэтгэлийг нэг үл мэдэгдэгчтэй шугаман тэгшитгэл гэнэ. Энд a , b нь тодорхой тоонууд харин x нь үл мэдэгдэгч болно.
Тэгшитгэлийг бодно гэдэг нь тэгшитгэлийг адитгал болгох x үл мэдэгдэгчийн тоон утгыг олно.

  1. Хэрэв a≠0 бол тэгшитгэлийн шийд нь
  2. Хэрэв a=0 бол хоёр тохиолдол гарна.
    • b=0 бол 0·x+0=0 энд x дурын тоо байж болно.
    • b≠0 бол 0·x+b=0 энд тэгшитгэл шийдгүй.

 

Энгийн бутархайн үйлдлүүд

  Нээгдсэн тоо: 5885 Бүртгүүлэх

Бутархайг өргөтгөх.

Бутархайн хүртвар ба хуваарийг 0 -ээс ялгаатай тоогоор үржүүлбэл бутархайн утга өөрчлөгдөхгүй. Энэ хувиргалтыг бутархайг өргөтгөх гэнэ. Жишээ нь



Бутархайг хураах.

Бутархайн хүртвар ба хуваарийг 0 -ээс ялгаатай тоонд хуваалбал бутархай өөрчлөгдөхгүй. Энэ үйлдлийг бутархайг хураах гэнэ. Жишээ нь

Вектор ба координат

  Нээгдсэн тоо: 9671 Төлбөртэй

Элсэлтийн ерөнхий шалгалтын материалд вектортой холбоотой бодлогууд орж ирэх нь элбэг байдгийн дээр геометрийн зарим бодлогуудыг векторын үйлдлүүдийг ашиглан их амархан шийдэх боломжтой. Иймээс энэ хичээлээр вектор, координатын суурь бодлогууд болох

  • Векторын координатыг түүний эхлэл ба төгсгөлийн координатаар хэрхэн олох
  • Координатууд нь өгөгдсөн үед векторын уртыг хэрхэн олох
  • Хоёр векторын нийлбэр, ялгавар векторын координатыг хэрхэн олох
  • Хэрчмийн дундажийн координатыг хэрхэн олох
  • Векторуудын скаляр үржвэр гэж юу болох
  • Вектор хоорондын өнцгийг хэрхэн олох

талаар авч үзэх юм. Эдгээр бодлогуудыг бодож сурсан байхад ЕБС-ийн хөтөлбөрт багтах вектортой холбоотой бүхий л бодлогыг шийдэх чадвартай болно. Огторгуй дахь вектор координатын үйлдлүүд хавтгайн дүрэмтэй яг ижлээр хийгддэг. Энд зөвхөн гуравдагч координат л нэмэгдэн орж ирдэг.

Үйл явдал…

Үйл явдал /event/ тодорхой үйлдэл хийгдсэн талаар системд мэдэгддэг. Хэрвээ бид энэхүү үйлдлийг ажиглах хэрэгтэй бол яг энд…

Нээгдсэн тоо : 304

 
Холбоосын параметрүүд

Манай төсөл олон хуудсуудтай болон тэдгээрийн хооронд динамикаар шилжилт хийж байгаа ч тухайн үед шилжилт хийгдсэн хуудаст тохирох…

Нээгдсэн тоо : 381

 
Зочин (Visitor)

Зочин (Visitor) паттерн классуудыг өөрчлөхгүйгээр тэдгээрийн обьектуудын үйлдлийг тодорхойлох боломжийг олгоно. Зочин хэвийг ашиглахдаа классуудын хоёр ангилалыг тодорхойлно.…

Нээгдсэн тоо : 350

 
Лямбда

Лямбда-илэрхийлэл нь нэргүй аргын хураангуй бичилтийг илэрхийлнэ. Лямбда-илэрхийлэл утга буцаадаг, буцаасан утгыг өөр аргын…

Нээгдсэн тоо : 443

 
Outlet компонент

Кодийн сайжруулалт /рефакторинг/ хичээлээр програмийн кодоо react -ийн зарчимд нийцүүлэн компонентод салгасан.…

Нээгдсэн тоо : 496

 
Хадгалагч (Memento)

Хадгалагч (Memento) хэв обьектын дотоод төлвийг түүний гадна гаргаж дараа нь хайрцаглалтын зарчмыг зөрчихгүйгээр обьектыг сэргээх боломжийг олгодог.

…

Нээгдсэн тоо : 514

 
Нэргүй арга

Делегаттай нэргүй арга нягт холбоотой. Нэргүй аргуудыг делегатийн хувийг үүсгэхэд ашигладаг.
Нэргүй аргуудын тодорхойлолт delegate түлхүүр үгээр…

Нээгдсэн тоо : 610

 
Урвуу матриц

Математикт харилцан урвуу тоонууд гэж бий. Ямар нэгэн тооны урвуу тоог олохдоо тухайн тоог сөрөг нэг зэрэг дэвшүүлээд…

Нээгдсэн тоо : 710

 
Кодийн сайжруулалт

Төсөлд react-router-dom санг оруулан чиглүүлэгчдийг бүртгүүлэн тохируулсан Санг суулган тохируулах хичээлээр бид хуудас…

Нээгдсэн тоо : 747

 
Энэ долоо хоногт
Бодлого 8.018

задаргааны хамгийн их нэмэгдхүүн бол a, b, c -г ол.

Нээгдсэн тоо : 1546

 
Бодлого 7.075

тэгшитгэлийг бод.

Нээгдсэн тоо : 1194

 
Бодлого 15.071

функцийн уламжлалын утгыг ол.

Нээгдсэн тоо : 447

 
© 2014 Зохиогчийн эрхээр хамгаалагдсан. Холбогдох - 96655195