Комбинаторикийн бодлогыг бодож сурах хэрэгтэй. Учир нь элсэлтийн ерөнхий шалгалтанд энэ сэдвийн бодлого орж ирэх нь гарцаагүй. Сэдэв өөрөө магадлалын онолын эхлэл болдог тул цаашдаа их дээд сургуульд үзэх хичээлүүдийн суурь тул сайн ойлгосон байх нь чухал. Эхний шатанд сэлгэмэл, гүйлгэмэл, хэсэглэлийн үндсэн томьёонуудын учрыг сайтар ойлгон тэдгээрийг бодлого бодоход хэрхэн яаж хэрэглэхийг сурсан байх шаардлагатай.
 n төрлийн обьект байлаа гэж үзье. Зургийг хар. Энд обьектудыг төлөөлүүлэн ердөө 3 төрлийн дүрсээр жишээ авъя. Эдгээр дүрсүүд дээр сэлгэмэл, гүйлгэмэл, хэсэглэл гэсэн ухагдхууныг авч үзнэ. Нийт обьектын тоо энд нэг их чухал биш гол утга учир ялгааг ойлгох нь чухал. Ухагдхууны ялгааг сайн ойлгоогүйгээс болоод ихэнх сурагчид ийм төрлийн бодлогыг бодохдоо хүндрэлтэй тулдаг.
n төрлийн обьект байлаа гэж үзье. Зургийг хар. Энд обьектудыг төлөөлүүлэн ердөө 3 төрлийн дүрсээр жишээ авъя. Эдгээр дүрсүүд дээр сэлгэмэл, гүйлгэмэл, хэсэглэл гэсэн ухагдхууныг авч үзнэ. Нийт обьектын тоо энд нэг их чухал биш гол утга учир ялгааг ойлгох нь чухал. Ухагдхууны ялгааг сайн ойлгоогүйгээс болоод ихэнх сурагчид ийм төрлийн бодлогыг бодохдоо хүндрэлтэй тулдаг.
Материалыг тусгай эрхтэй хэрэглэгч үзнэ.
request_quoteТусгай эрх авах




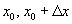 цэгүүд дээрх
цэгүүд дээрх 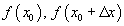 утгуудыг авч үзье.
утгуудыг авч үзье. 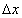 -г
-г 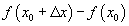
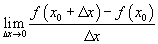 хязгаарыг x0 цэг дээрх f(x) функцын
хязгаарыг x0 цэг дээрх f(x) функцын 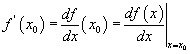 гэж тэмдэглэдэг.
гэж тэмдэглэдэг.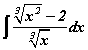 интеграл бод
интеграл бод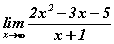 хязгаарыг бод.
хязгаарыг бод.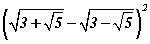 утгыг ол.
утгыг ол.