
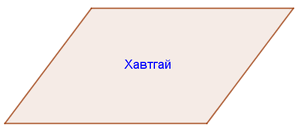
Геометр амьдралд ойр хэдий ч математик дотроо хамгийн адармаатай болоод төвөгтэй хэсэг. Энэ ч утгаараа сурагчдад геометрийн бодлогууд нилээд асуудлыг үүсгэдэг. Геометрийн сэдвийн суурь ухагдхуунуудыг муу эсхүл дутуу ойлгосноос энэхүү хүндрэл үүсэх шалтгаан байдаг гэж үзэн Хавтгайн геометрийн ухагдхуунуудын талаар багц хичээлийг бэлтгэн танилцуулж байгааг хүлээн авна уу. Хичээлд хавтгайн геометрийн бүхий л ухагдхуунуудыг аль болохоор энгийн болоод товчоор ойлгуулахыг хичээлээ. Суурь ухагдхуунуудыг мэдэхгүй эсхүл ойлгоогүй бол геометрийн бодлогыг бодох тухай санах ч хэрэггүй болов уу. Жишээ нь хавтгай, шулуун, периметр, багтсан тойрог, биссектрис, медиан, төв өнцөг, гадаад өнцөг гэх мэтийн ухагдхуунууд юуг илэрхийлдэг, ямар шинж, чанартайг мэдэхгүйгээр бодлого бодох гэвэл "үсэг мэдэхгүйгээр" уншина гэсэн адил хэрэг юм. Хичээлүүдийг багцаар нь нэг дороос үзэх нь таны цаг, завыг хэмнэх цаашлаад манай сайтын үндсэн зорилго болсон бие даан суралцах чадвар ойлгохтой нийцэж байгаа болно.
Зарим хичээлүүд төлбөртэй тул та хичээлүүдийг бүгдийг үзэхийн тулд Тусгай эрхтэй хэрэглэгч байх ёстойг анхаарна уу.
Танд амжилт хүсье.






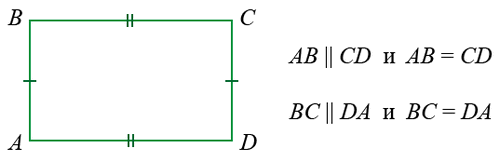
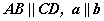 бичлэгийг AB шулуун CD шулуунтай паралел, a шулуун b шулуунтай паралел гэж уншин ойлгож сураарай.
бичлэгийг AB шулуун CD шулуунтай паралел, a шулуун b шулуунтай паралел гэж уншин ойлгож сураарай.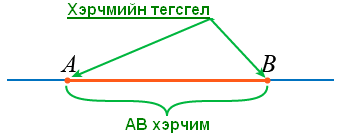
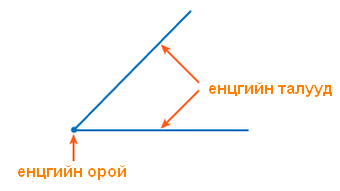
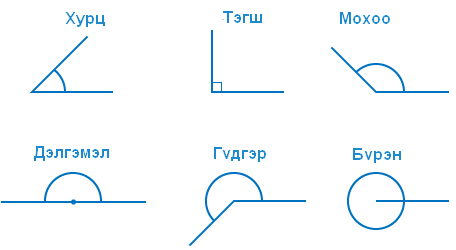
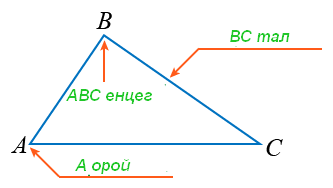
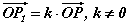 гэсэн P1 цэгээр илэрхийлэгдэх хувиргалт юм.
гэсэн P1 цэгээр илэрхийлэгдэх хувиргалт юм.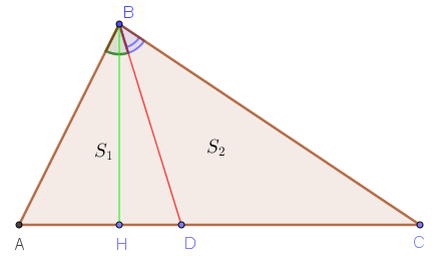
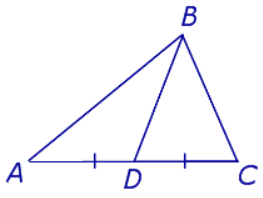

 функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол. тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.