Тойргуудын харилцан байршил

Хоёр тойрогийн харилцан байршлыг тэдгээрийн радиусууд R, r болон төв хоорондын зай d гээр харьцуулан тодорхойлохыг авч үзье. Тодорхой байх үүднээс R≥r гэж үзье. Тойргууд харилцан байрших байрлалуудыг авч үзвэл

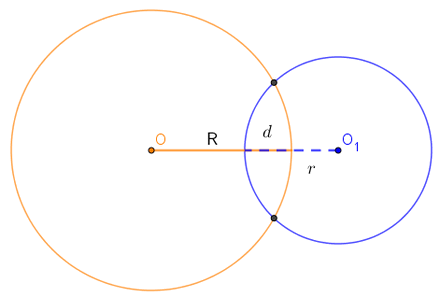Огтлолцсон тойргууд хоёр ерөнхий цэгтэй байна.

Тойрогийн төв хоорондын зай тэгээс их байгаад түүний хэмжээ тойргуудын радиусуудийн ялгавар ба нийлбэрийн дунд байвал тойргууд хоёр цэгт огтлолцоно.

Математик тэмдэглэгээгээр тодорхойлбол R > r, d>0 бол R-r < d < R+r нөхцөл биелж байхад тойргууд хоёр цэгт огтлолцоно.

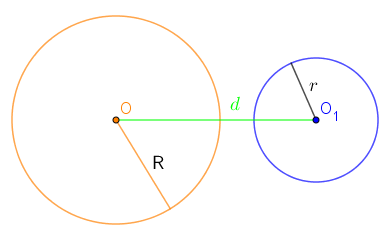Огтлолцоогүй тойргууд ерөнхий цэггүй.

Тойргууд огтлолцохгүйгээр гурван янзаар байрлаж болно.

1-р хувилбар.

Нэг тойрог нөгөөгийнхөө гадна байрлах.
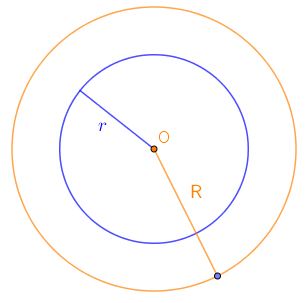Хэрвээ тойрогийн төв хоорондын зай тэгээс их байгаад тойргуудын радиусийн нилбэрээс их байвал нэг тойрог нөгөөгийнхөө гадна байрлана.
Өөрөөр хэлбэл d > R+r

2-р хувилбар

Нэг тойрог нөгөөгийнхөө дотор байрлан тэдгээрийн төвүүд нь давхцсан.

Тойргуудын төв хоорондын зай нь тэгтэй тэнцэх тойргуудыг төвлөрсөн тойргууд гэж нэрлэдэг. Нэршлийг арай өөрөөр хэлдэг байж магадгүй.
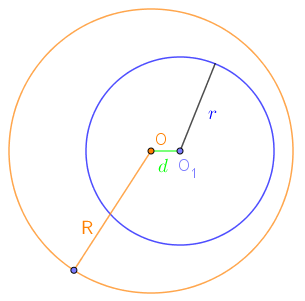Өөрөөр хэлбэл тойргуудын төвүүд давхцаж байвал төв хоорондын зай тэг бөгөөд богино радиустай тойрог их радиустай тойргийн дотор байрлана.

3-р хувилбар

Нэг тойрог нөгөөгийнхөө дотор байрласан ч тэдгээрийн төвүүд нь давхцаагүй.

Тойргуудын төв хоорондын зай нь тэгтэй тэнцэхгүй бөгөөд тойргуудын радиусуудийн ялгавараас бага байвал богино радиустай тойрог их радиустай тойргийн дотор байрлана.
Өөрөөр хэлбэл d < R-r

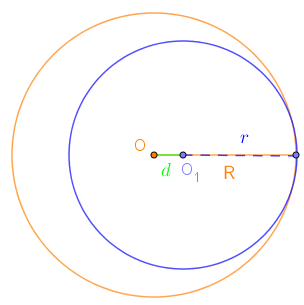Тойргууд ерөнхий нэг цэгтэй байвал тэдгээрийг шүргэлцсэн тойргууд гэнэ.

Энд дотоод ба гадаад гэсэн хоёр тохиолдол бий.

Шүргэлцсэн тойргуудын төвүүд болон тэдгээрийн ерөнхий цэг нэг шулуун дээр байрлана.

Дотоод шүргэлцэл

Тойргуудын төвүүд хоорондын зай тэгээс их байгаад радиусуудийн ялавартай тэнцүү бол тойргуудыг дотоод шүргэлцсэн гэнэ.
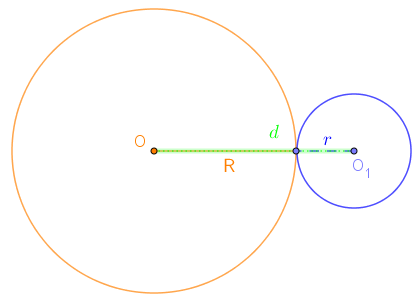Өөрөөр хэлбэл R>r, d>0 бол d=R-r байна гэсэн үг.

Гадаад шүргэлцэл

Тойргуудын төвүүд хоорондын зай тэгээс их байгаад радиусуудийн нийлбэртэй тэнцүү бол тойргуудыг гадаад шүргэлцсэн гэнэ.
Өөрөөр хэлбэл R>r, d>0 бол d=R+r байна гэсэн үг.

Мэдээлэл таалагдсан бол найзуудтайгаа хуваалцаарай.

Холбоотой материалууд
Нийлбэрийг өөрчлөх

  Нээгдсэн тоо: 407 Бүртгүүлэх

Нэмэгдхүүнүүдийн байрыг сэлгэх, нэгтгэх, бүлэглэх дүрмүүд нийлбэрийн тооцоог хялбар болгоход голлон ашиглагддаг бол нэмэгдхүүний өөрчлөлтөөр нийлбэрийг өөрчлөх шинж нь илэрхийллийг хялбарчлах, адитгал хувиргалтын суурь болдог. Иймээс хичээлийн материалыг сайтар судлан ойлгон авахыг хичээгээрэй.

Гурван үл мэдэгдэгчтэй гурван шугаман тэгшитгэлийн систем

  Нээгдсэн тоо: 6802 Бүртгүүлэх

хэлбэрийн тэгшитгэлийн системийг гурван үл мэдэгдэгчтэй гурван шугаман тэгшитгэлийн систем гэнэ. Энд a, b, c, d, e, f, g, h, p, q, r, s өгөгдсөн тоонууд, x, y, z үл мэдэгдэгчид. a, b, c, e, f, g, p, q, r  үл мэдэгдэгчдийн коэффициент, d, h, s сул гишүүд юм. Ийм тэгшитгэлийн системийг үндсэн хоёр аргаар /орлуулах, нэмэх ба хасах/ боддог. Энд бид зөвхөн Крамерын аргыг дэлгэрэнгүй авч үзнэ. Эхлээд гуравдугаар эрэмбийн тодорхойлогч гэдэг ойлголтыг авч үзье. Дараах илэрхийллийг

Тригнометрийн бодолтын жишээ

  Нээгдсэн тоо: 2741 Төлбөртэй

Энэ нийтлэлээр бодит шалгалт дээр ирж байсан тригнометрийн хоёр бодлогын бодолтыг дэлгэрэнгүйгээр тайлбарлах болно. Эдгээр бодлогын бодолтыг сайн судлаад ойлговол тригнометрийн бодлогыг ойлгоход сайн суурь болж чадна. Бодлогын шийдүүдээс өгөгдсөн завсар дахь утгуудыг сонгох нэмэлт нөхцөл оруулсан нь сурагчдаас тригнометрийн илүү нарийн ойлголтыг шаардах юм. Сурагчид бодлогыг хураангуйлан энгийн хэлбэрт оруулж чаддаг ч шийдийг гаргах тэр тусмаа өгөгдсөн завсарт харьяалагдах шийдийг сонгохдоо үндсэн хүндрэлтэй тулдаг. Иймд бодолтуудыг анхааралтай судлаад ойлгон авахыг хичээгээрэй. Олон бодлого бодохдоо биш аргачлалыг ойлгох нь чухал.

Хоёр үл мэдэгдэгчтэй хоёр шугаман тэгшитгэлийн систем

  Нээгдсэн тоо: 3351 Төлбөртэй

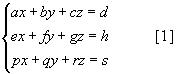хэлбэрийн тэгшитгэлийн системийг 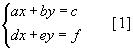хоёр үл мэдэгдэгчтэй хоёр шугаман тэгшитгэлийн систем гэнэ.Энд a, b, c, d, e, f нь өгөгдссөн тоонууд. x, y нь үл мэдэгдэгчид. a, b, c, d тоонууд нь үл мэдэгдэгчдийн коэффициентүүд, e, f сул гишүүд. Ийм тэгшитгэлийн системийг үндсэн хоёр аргаар боддог.

Орлуулах арга

  1. Аль нэг тэгшитгэлээс аль нэг үл мэдэгдэгчийг жишээлбэл x-г нөгөө үл мэдэгдэгч y болон коэффициентүүдээр илэрхийлнэ. x=(c-by)/a [ 2 ]
  2. Хоёрдугаар тэгшитгэлд x -ийг орлуулж бичнэ. d(c-by)/a+ey=f
  3. Сүүлчийн тэгшитгэлээс y-г олно. y=(af-cd)/(ae-bd)
  4. y-ийн утгыг [ 2 ] илэрхийлэлд орлуулна. x=(ce-bf)/(ae-bd)
Үйл явдал…

Үйл явдал /event/ тодорхой үйлдэл хийгдсэн талаар системд мэдэгддэг. Хэрвээ бид энэхүү үйлдлийг ажиглах хэрэгтэй бол яг энд…

Нээгдсэн тоо : 292

 
Холбоосын параметрүүд

Манай төсөл олон хуудсуудтай болон тэдгээрийн хооронд динамикаар шилжилт хийж байгаа ч тухайн үед шилжилт хийгдсэн хуудаст тохирох…

Нээгдсэн тоо : 369

 
Зочин (Visitor)

Зочин (Visitor) паттерн классуудыг өөрчлөхгүйгээр тэдгээрийн обьектуудын үйлдлийг тодорхойлох боломжийг олгоно. Зочин хэвийг ашиглахдаа классуудын хоёр ангилалыг тодорхойлно.…

Нээгдсэн тоо : 339

 
Лямбда

Лямбда-илэрхийлэл нь нэргүй аргын хураангуй бичилтийг илэрхийлнэ. Лямбда-илэрхийлэл утга буцаадаг, буцаасан утгыг өөр аргын…

Нээгдсэн тоо : 432

 
Outlet компонент

Кодийн сайжруулалт /рефакторинг/ хичээлээр програмийн кодоо react -ийн зарчимд нийцүүлэн компонентод салгасан.…

Нээгдсэн тоо : 481

 
Хадгалагч (Memento)

Хадгалагч (Memento) хэв обьектын дотоод төлвийг түүний гадна гаргаж дараа нь хайрцаглалтын зарчмыг зөрчихгүйгээр обьектыг сэргээх боломжийг олгодог.

…

Нээгдсэн тоо : 505

 
Нэргүй арга

Делегаттай нэргүй арга нягт холбоотой. Нэргүй аргуудыг делегатийн хувийг үүсгэхэд ашигладаг.
Нэргүй аргуудын тодорхойлолт delegate түлхүүр үгээр…

Нээгдсэн тоо : 599

 
Урвуу матриц

Математикт харилцан урвуу тоонууд гэж бий. Ямар нэгэн тооны урвуу тоог олохдоо тухайн тоог сөрөг нэг зэрэг дэвшүүлээд…

Нээгдсэн тоо : 690

 
Кодийн сайжруулалт

Төсөлд react-router-dom санг оруулан чиглүүлэгчдийг бүртгүүлэн тохируулсан Санг суулган тохируулах хичээлээр бид хуудас…

Нээгдсэн тоо : 726

 
Энэ долоо хоногт
Бодлого 9.010

a ба b катеттай тэгш өнцөгт гурвалжин ерөнхий тэгш өнцөгтэй квадратыг багтаасан бол квадратын периметрийг ол.

Нээгдсэн тоо : 1133

 
Бодлого 15.055

функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.

Нээгдсэн тоо : 748

 
Бодлого 5.078

тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.

Нээгдсэн тоо : 820

 
© 2014 Зохиогчийн эрхээр хамгаалагдсан. Холбогдох - 96655195