Геометрийг ойлгоход өнцөг ойлголт ихээхэн чухал. Бодлогын нөхцөлд өнцгүүдийн төрлүүд их орж ирдэг тул тэдгээрийг нэр, хэлбэр, шинжээр нь мэдэж байх хэрэгтэй. Өнцгүүд өөрийн хэмжээнээс хамааран тусдаа нэрүүдтэй.
Геометрийн ухагдхуунуудыг сайн ойлгохгүйгээр бодлогод тэдгээрийг ашиглах бараг боломжгүй тул Хавтгайн геометр хичээлийн багцыг үзэхийг зөвлөе.
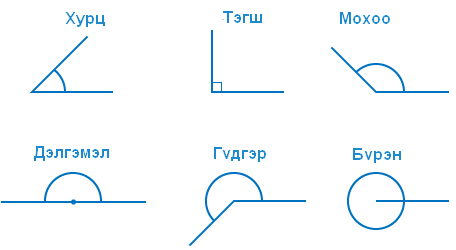
- Хэмжээ нь 90 градусаас бага өнцгийг хурц өнцөг гэнэ.
- Талууд нь бие биедээ перпендикуляр өнцгийг тэгш өнцөг гэнэ. Тэгш өнцгийг d үсгээр тэмдэглэдэг бөгөөд 900 -тай тэнцүү. Тэгш өнцгийг ихэнхдээ нумаар биш булангаар тэмдэглэдэг.
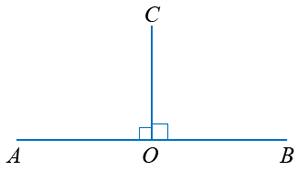
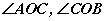 тэгш өнцгүүд. Өнцгүүдийн ерөнхий OC талыг AB шулууны перпендикуляр гэж нэрлэх ба O цэгийг перпендикулярийн суурь гэдэг. Хоёр тэгш өнцгийн нийлбэр дэлгэмэл өнцөгтэй тэнцүү тул тэгш өнцөг нь дэлгэмэл өнцгийн хагастай тэнцүү.
тэгш өнцгүүд. Өнцгүүдийн ерөнхий OC талыг AB шулууны перпендикуляр гэж нэрлэх ба O цэгийг перпендикулярийн суурь гэдэг. Хоёр тэгш өнцгийн нийлбэр дэлгэмэл өнцөгтэй тэнцүү тул тэгш өнцөг нь дэлгэмэл өнцгийн хагастай тэнцүү. - Тэгш өнцгөөс их дэлгэмэл өнцгөөс бага хэмжээтэй өнцгийг мохоо өнцөг гэнэ. Өөрөөр хэлбэл хэмжээ нь 90 градусаас их 180 градусаас бага гэсэн үг.
- Хоёр нэмэлт цацрагаар үүссэн өнцгийг дэлгэмэл өнцөг гэнэ. Дэлгэмэл өнцөг хоёр тэгш өнцөгтийн нийлбэртэй тэнцүү буюу 2d эсхүл 180 градус байна.
- Дэлгэмэл өнцгөөс их ч бүрэн өнцгөөс бага хэмжээтэй өнцгийг гүдгэр өнцөг гэнэ. Өөрөөр хэлбэл 180 ба 360 градусийн хооронд хэмжээтэй өнцөг.
- Өнцгийн хоёр тал нэг цацрагт давхацсан өнцгийг бүрэн өнцөг гэнэ. Бүрэн өнцөг дөрвөн тэгш өнцөгт 4d буюу 360 градустай тэнцэнэ.
Санамж: Дээрх зурагт үзүүлсэн өнцгүүдийн нэр, шинжүүдийг цээжээр мэдэж байх хэрэгтэй. Учир нь бодлогын нөхцөлд өнцгүүдийг нэрээр нь ихээр өгдөг. Хэрвээ өнцгийн нэрээр тухайн өнцгийг ямар хэлбэртэйг шууд тодорхойлж чадахгүй бол хүнд асуудалд орно гэдгийг сануулъя. Сурагчид хурц, тэгш, мохоо өнцгөөс бусдыг сайн мэддэггүй.
Зэргэлдээ өнцгүүд
Зэргэлдээ өнцгүүд гэдэг нь ерөнхий орой ба талтай харин нөгөө талууд нь ерөнхий талын эсрэг талуудад байрлах хос өнцгийг хэлнэ.
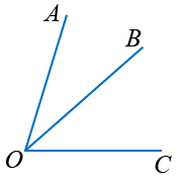
 - зэргэлдээ өнцгүүд. O - ерөнхий орой, OB - ерөнхий тал.
- зэргэлдээ өнцгүүд. O - ерөнхий орой, OB - ерөнхий тал.
Дурын өнцгийн оройгоос өнцгийг хоёр хэсэгт хуваах цацрагийг татвал үүсэх өнцгүүд зэргэлдээ өнцгүүд байна. Цацрагаар хуваагдсан өнцгийг үүссэн өнцгүүдийн нийлбэр гэж нэрлэнэ.
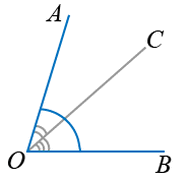
AOB нь AOC, COB өнцгүүдийн нийлбэр юм. Өөрөөр хэлбэл 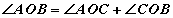 гэсэн үг. Эндээс AOC, COB өнцгүүдийг AOB өнцөг нөгөө нэг зэргэлдээ өнцгийн ялгавар гэж нэрлэдэг.
гэсэн үг. Эндээс AOC, COB өнцгүүдийг AOB өнцөг нөгөө нэг зэргэлдээ өнцгийн ялгавар гэж нэрлэдэг. 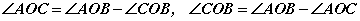





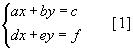 хэлбэрийн тэгшитгэлийн системийг
хэлбэрийн тэгшитгэлийн системийг 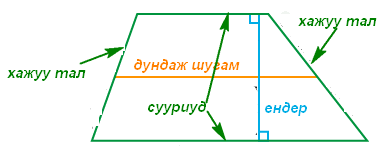
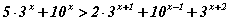 тэнцэтгэл бишийг бод.
тэнцэтгэл бишийг бод.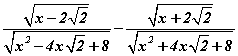 илэрхийллийн x=3 утгыг ол.
илэрхийллийн x=3 утгыг ол.