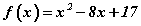функц өгөгдөв.
- f(x) функцын x0=5 абсцисстай M цэгт татсан шүргэгч шулууны тэгшитгэл
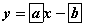
- f(x) функцын график, дээрх шүргэгч шулуун болон координатын тэнхлэгүүдээр хүрээлэгдсэн дүрсийн талбай
- f(x) функцын графикийг M цэгт шүргэх, төв нь OX (абсцисс) тэнхлэг дээр орших тойргийн тэгшитгэл
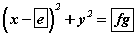
Материалыг тусгай эрхтэй хэрэглэгч үзнэ.
request_quoteТусгай эрх авах
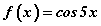функцийн уламжлалыг ол.
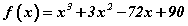функцын уламжлалын утгыг ол.
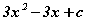функцийн графикийн шүргэгч бол с -г ол.
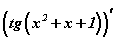ол.
задаргааны хамгийн их нэмэгдхүүн 
бол a, b, c -г ол.
тэгшитгэлийг бод.
функцийн уламжлалын 
утгыг ол.