Хаалттай тахир шугаман дүрсүүд периметр, талбайтай байдаг. Гурвалжин ч хаалттай тахир шугамаар үүсдэг дүрс тул хичээлээр гурвалжны периметр, талбайн талаар авч үзье.
Жич: Геометрийн бодлогод периметр, талбайг ол гэсэн нөхцөл байхаас тухайн ухагдхуун гэж юу болох хэрхэн тооцохыг та өөрөө мэдэж байхыг шаардана. Ухагдхууныг мэдэхгүй, яаж тооцохыг мэдэхгүй бол бодлогыг бодохгүй л гэсэн үг.
Периметр
Ямарч гурвалжны периметр түүний гурван талын нийлбэртэй тэнцүү. Гурвалжны периметрийг олох ерөнхий томьёо
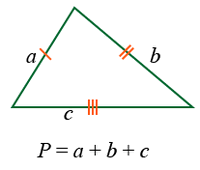
P=a+b+c юм. Энд P - периметр харин a, b, c - гурвалжны талуудын урт. Адил хажуут гурвалжны хувьд хоёр тал нь өөр хоорондоо тэнцүү гэдгээс периметрийг P=2a+b томьёогоор харин адил талт гурвалжны гурван тал тэнцүү тул P=3a томьёогоор олно. Сүүлийн хоёр томьёо ерөнхий томьёоны тухайн тохиолдол гэдгийг дурдая. Энд бас л гурвалжны гурван талын уртын нийлбэр гэдэг нь ойлгомжтой.
Талбай
Гурвалжны талбайг түүний суурь болон түүнд буулгасан өндрөөр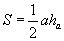 
томьёогоор олдог. Гурвалжин хичээлээс дурын гурвалжин гурван өндөртэй байдагийг мэдэх тул түүний талбайг дурын нэг тал түүнд буулгасан өндөрөөр олох боломжтой гэдгийг тогтоон аваарай. Өндөр буулгсан талыг суурь гэж хэлнэ.
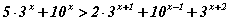тэнцэтгэл бишийг бод.
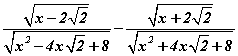илэрхийллийн x=3 утгыг ол.