Хавтгайн геометрт хамгийн өргөн хэрэглэдэг дүрс бол гурвалжин. Гурвалжны шинж чанарууд бараг бүх бодлогод орж ирдэг гэхэд хилсдэхгүй. Иймээс гурвалжны шинж, чанаруудыг сайн ойлгон тогтоон авбал цаашид их хэрэгтэйг зөвлөе.
Гурвалжин гэдэг нь гурван холбоосоос бүрдсэн хаалттай тахир шугам. Тодорхойлолтыг тахир шугам хичээлийг үзэн зөв ойлгон тогтоож аваарай.
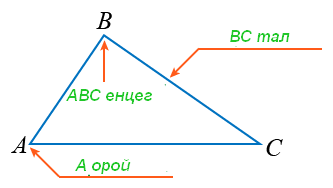
Тахир шугамын оройнуудыг гурвалжны орой харин түүний холбоосуудыг гурвалжны талууд гэнэ. Гурвалжны талуудаар үүсэх өнцгүүдийг гурвалжны оройн өнцгүүд гэж нэрлэнэ. Зурагт үзүүлсэн ABC тахир шугам гурвалжин үүсгэсэн бөгөөд түүний A, B, C оройнууд гурвалжны оройнууд, AB, BC, CA холбоосууд гурвалжны талууд болно. 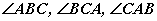 - гурвалжны өнцгүүд ба тэдгээрийг бас харгалзах оройн үсгээр
- гурвалжны өнцгүүд ба тэдгээрийг бас харгалзах оройн үсгээр 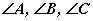 гэж ч тэмдэглэдэг.
гэж ч тэмдэглэдэг.
Гурвалжинг түүний оройнуудын гурван үсгээр голдуу тэмдэглэдэг. Жишээ нь ABC эсхүл BCA эсхүл CBA гурвалжин гэнэ. Гурвалжин үгийн оронд тэмдэг ашиглан 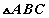 гэж ч тэмдэглэдэг.
гэж ч тэмдэглэдэг.
Гурвалжин бүр 3 орой, 3 тал, 3 өнцөгтэй.
Өндөр
Гурвалжны аль нэг оройгоос түүний эсрэг орших талд буулгасан перпендикулярийг гурвалжны өндөр гэнэ. Гурвалжны өндөр талын үргэлжлэлд бууж болно.
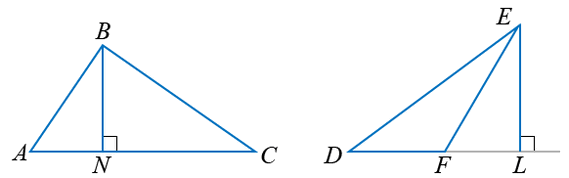
BN хэрчим ABC гурвалжны өндөр. Харин EL хэрчим DEF гурвалжны DF талын үргэлжлэлд буулгасан өндөр.
Оройн өнцөг болон эсрэг орших талтай огтлолцсон цэгээр үүссэн хэрчмийн уртыг гурвалжны өндөрийн урт гэнэ. Эндээс гурвалжин болгон гурван өндөртэй байна гэсэн дүгнэлтийг хийж болно.
Биссектрис
Гурвалжны оройн өнцгийг таллан хуваасан шулууныг гурвалжны биссектрис гэнэ. Оройн өнцгийг хуваасан шулууны оройн өнцгөөс эсрэг орших талтай огтлолцох цэг хүртэлх хэрчмийн уртыг биссектрисийн урт гэдэг.
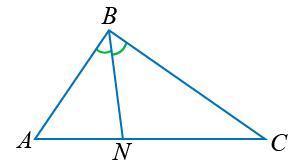
BN хэрчим нь ABC гурвалжны биссектрис. Гурвалжин бүр гурван биссектристэй.
Медиан
Гурвалжны оройг түүний эсрэг орших талын дундажтай холбосон хэрчмийг гурвалжны медиан гэнэ. Энэ хэрчмийн уртыг медианий урт гэдэг. Гурвалжин бүр гурван медиантай.
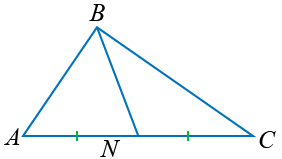
BN хэрчим нь ABC гурвалжны медиан.
Дундаж шугам
Гурвалжны хоёр талын дундажийг холбосон шугамыг тухайн гурвалжны дундаж шугам гэдэг.
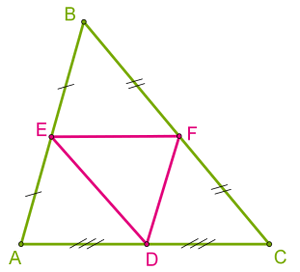
Гурвалжны дундаж шугам түүний аль нэг талтай паралел байхын дээр энэ талын хагастай тэнцүү. Өөрөөр хэлбэл AC||EF, AB||FD, BC||ED ба EF=AC/2, FD=AB/2, ED=BC/2 гэсэн үг. Гурвалжин бүр гурван дундаж шугамтай.
Гурвалжны эдгээр хэрчмүүд хэрхэн үүсдэг ямар нэртэйг шууд цээжлэх хэрэгтэй. Хичээлээр үзсэн гурвалжин, түүний чухал хэрчмийн тухай ойлголт эхний удаад хангалттай гэж үзээд үүгээр дуусгая. Хичээлийг аль болохоор энгийн болоод ойлголтуудыг бага хэмжээгээр оруулах байдлаар боловсруулсан тул хичээл бүрд өгч буй ухагдхууныг бүрэн ойлгон тогтоон авахыг зөвлөе.





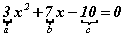 a - квадрат зэрэгтэй гишүүний, b - нэгдүгээр эрэмбийн гишүүний , c - сул гишүүн гэж тэмдэглэе.
a - квадрат зэрэгтэй гишүүний, b - нэгдүгээр эрэмбийн гишүүний , c - сул гишүүн гэж тэмдэглэе.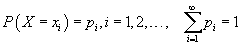
 функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол. тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.