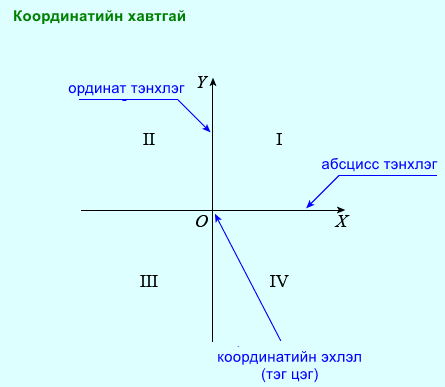
Үржих үйлдэлд байр сэлгэх, бүлэглэх, гишүүнчлэн үржүүлэх гэсэн дүрмүүд үйлчилдэг. Эдгээрийг эхнээс нь сайн ойлгон цээжлэх хэрэгтэй.
Байр сэлгэх
Үржигдхүүн болон үржигчийн байрыг солиход үржвэр өөрчлөгдөхгүй нь доорх зураг дээрх однуудын тоог гаргаж буй хоёр аргаас харагдана.

Үржих бол ижил бүрдүүлэгчдийн нийлбэрийг олох арифметик үйлдэл тул дээрх зураг дээрх однуудын нийт тоог 3·4 эсхүл 4·3 үржвэрээр олох боломжтой. Үржигдхүүн болон үржигчийн байрыг солих боломжтой тул тэдгээрийг үржигдхүүнүүд гэж ч бас нэрлэдэг.
Материалыг бүртгэлтэй хэрэглэгч үзнэ.
how_to_regБүртгүүлэх




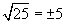 Учир нь (+5)2=25 бас (-5)2=25 байдаг.
Учир нь (+5)2=25 бас (-5)2=25 байдаг.  функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол. тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.