Алгебрт тоон эсхүл координатийн тэнхлэг ойлголт чухал үүрэгтэй. Иймээс хичээлээр тоон тэнхлэг ухагдхууны талаар авч үзье.
Эхлэлийн цэг, эерэг чиглэл болон нэгж хэрчмийг тэмдэглэсэн шулууныг координатийн буюу тоон тэнхлэг гэнэ. O эхлэлийн цэгтэй эерэг чиглэлийг сумаар заасан доорх шулууныг авч үзье.
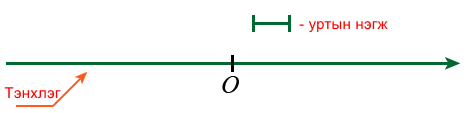
Шулуунд уртын нэгжээр дурын хэрчмийг сонгоё. Ийм шулууныг тэнхлэг гэж нэрлэнэ.
Тэнхлэгт O цэгээс уртын нэгжээр (дурын байдлаар сонгосон хэрчим) баруун болон зүүн чиглэлд 1, 2, 3, 4, 5 гэх мэтээр хэрчим үүсгэн тэмдэглээд хэрчим бүрийн төгсгөлд эерэг чиглэлд +1, +2 харин зүүн тийш -1, -2 гэх мэтээр тоонуудыг тавья. Ийм тэнхлэгийг тоон тэнхлэг гэнэ.
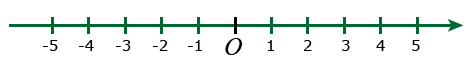
Тэнхлэгт 0 нь O цэгтэй давхцана. Ингэснээр эерэг, сөрөг, эсхүл тэг дурын тоог тэнхлэгт зөвхөн нэг цэгээр төлөөлүүлэн үзүүлж болно.
Цэг ба тоо нь өөр ойлголтууд. Тухайн цэгт тавигдсан тоо бол O цэгээс тухайн цэг хүртлэх уртын нэгжээр илэрхийлэгдэх зай юм. Жишээ нь O цэгээс баруун тийш буюу эерэг чиглэлд тавигдсан 2,5 тоо нь цэг O цэгээс 2,5 уртын нэгж зайтайг илэрхийлнэ. Үүнийг "цэг 2,5 тоонд харгалзана", "цэг 2,5 -ийг дүрслэнэ" эсхүл "2,5 цэг" гэж ч ярьдаг.

Тодорхой цэгт харгалзах тоог энэ цэгийн координат гэдэг. Тэнхлэгт бүх цэгүүд тодорхой координатттай учраас ийм шулууныг координатийн тэнхлэг эсхүл координатийн шулуун ч гэж бас нэрлэдэг.





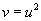 гэсэн функц байсан гэе. Энд u нь аргумент, v нь функц. Хэрвээ эдгээрийн үүргийг соливол v ээс хамаарсан u функц гарна.
гэсэн функц байсан гэе. Энд u нь аргумент, v нь функц. Хэрвээ эдгээрийн үүргийг соливол v ээс хамаарсан u функц гарна. 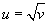
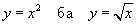 гэсэн нэг нь нөгөөдөө урвуу хоёр функц гарна.
гэсэн нэг нь нөгөөдөө урвуу хоёр функц гарна.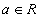 энэ бичлэг нь a нь R олонлогийн элемент ба энэ олонлогт харьяалагдана гэснийг илэрхийлнэ. Эсрэгээр a нь R олонлогт харьяалагдахгүй гэдгийг
энэ бичлэг нь a нь R олонлогийн элемент ба энэ олонлогт харьяалагдана гэснийг илэрхийлнэ. Эсрэгээр a нь R олонлогт харьяалагдахгүй гэдгийг 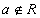 гэж бичнэ.
гэж бичнэ.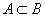 гэж бичнэ. Дурын A олонлогийн хувьд
гэж бичнэ. Дурын A олонлогийн хувьд 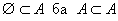 багтаалт хүчинтэй.
багтаалт хүчинтэй.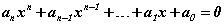 хэлбэрээр өгөгдсөн тэгшитгэлийг ойлгоно. Энд an, an-1, ... , a0 - өгөгдсөн тоонууд, x - үл мэдэгдэгч, n - үл мэдэгдэгчийн хамгийн их зэрэг буюу алгебрийн тэгшитгэлийн зэрэг гэж нэрлэнэ. Алгебрийн тэгшитгэлүүдийн төрлүүд болон тэдгээрийг бодох аргуудтай танилцгаая.
хэлбэрээр өгөгдсөн тэгшитгэлийг ойлгоно. Энд an, an-1, ... , a0 - өгөгдсөн тоонууд, x - үл мэдэгдэгч, n - үл мэдэгдэгчийн хамгийн их зэрэг буюу алгебрийн тэгшитгэлийн зэрэг гэж нэрлэнэ. Алгебрийн тэгшитгэлүүдийн төрлүүд болон тэдгээрийг бодох аргуудтай танилцгаая.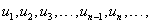 тэмдэглэгээ
тэмдэглэгээ 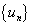
 функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол. тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.