x=sin y харьцаагаар x -ийн өгөдсөн утгаар y -ийг, y -ийн өгөдсөн утгаар x (|x|≤1) -ийг олж болно. Иймээс синусыг өнцгийн функцээс гадна өнцгийг синусын функц мэтээр авч үзэж болно. Үүнийг y=arcsin x / arcsin – арксинус гэж уншина / гэж бичиж болно. Жишээ нь, 1/2=sin 30° гэхийн оронд 30°=arcsin 1/2 гэж бичиж болно. Сүүлийн бичлэгийн хувьд өнцгийг голдуу радианаар π/6=arcsin 1/2 гэж бичдэг.
Синус нь x тэй тэнцүү өнцгийг arcsin x гэнэ. arccos x, arctan x, arccot x, arcsec x, arccosec x функцүүд бүгдээрээ arcsin x тэй адилхан тодорхойлогдоно. Эдгээр функцүүд нь sin x, cos x, tan x, cot x, sec x, cosec x функцүүдтэй эсрэг харьцаатай байдаг тул тригнометрийн урвуу функцүүд гэдэг.
Бүх эсрэг функцүүд нь олон утгатай. Учир нь аргументын утга бүрт функцийн хязгааргүй олон утга харгалзана. Жишээ нь, 30°, 150°, 390°, 510°, 750° г.м өнцгүүдэд синусын ганцхан утга харгалзана.
Эсрэг функцүүдийн үндсэн утгын мужууд:
- arcsin x - -π/2 ≤ arcsin x ≤ +π/2
- arccos x - 0 ≤ arccos x ≤ π
- arctan x - -π/2 < arctan x <+π/2
- arccot x - 0 < arccot x <π
Тригнометрийн эсрэг функцүүдийн дурын утгыг Arcsin x, Arccos x, Arctan x, Arccot x, үндсэн утгуудыг arcsin x, arccos x, arctan x, arccot x гэж тэмдэглэвэл эдгээр нь дараах харьцаагаар илэрхийлэгдэнэ.
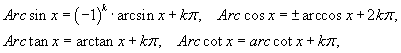
k бүхэл тоо. k=0 үед үндсэн утга гарна.
Урвуу функцүүдын үндсэн харьцаанууд
Тригнометрийн эсрэг функцүүдын үндсэн харьцаанууд. Доорх томьёонуудад орсон бүх квадрат язгуурууд нь эерэг тоонууд.
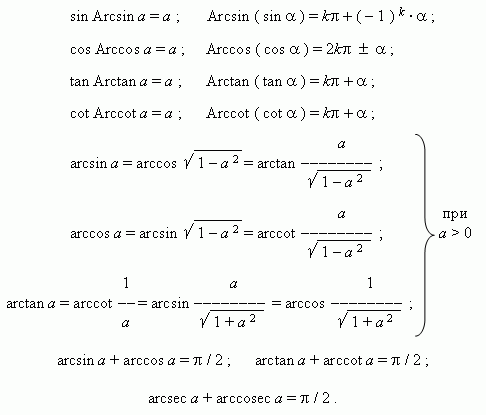





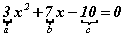 a - квадрат зэрэгтэй гишүүний, b - нэгдүгээр эрэмбийн гишүүний , c - сул гишүүн гэж тэмдэглэе.
a - квадрат зэрэгтэй гишүүний, b - нэгдүгээр эрэмбийн гишүүний , c - сул гишүүн гэж тэмдэглэе.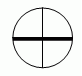
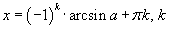
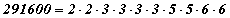 болно. Эндээс тооцоог хийвэл
болно. Эндээс тооцоог хийвэл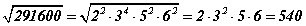 гээд л болоо. Тоо 2, 3, 4 гэх мэтээр үржигдхүүнд задарвал арга нь дажгүй. Гэхдээ нэг асуудал бий. Язгуураас гаргах тоо маань анхны тоонуудыг үржвэр хэлбэрээр задарч байвал яах вэ? Жишээ нь 152881 нь 17·17·23·23 гэж задарна. Эдгээр хуваагчийг шууд олох гээд үзээрэй. Нилээд хүндхэн байх болов уу.
гээд л болоо. Тоо 2, 3, 4 гэх мэтээр үржигдхүүнд задарвал арга нь дажгүй. Гэхдээ нэг асуудал бий. Язгуураас гаргах тоо маань анхны тоонуудыг үржвэр хэлбэрээр задарч байвал яах вэ? Жишээ нь 152881 нь 17·17·23·23 гэж задарна. Эдгээр хуваагчийг шууд олох гээд үзээрэй. Нилээд хүндхэн байх болов уу. илэрхийллийг хялбарчил.
илэрхийллийг хялбарчил.
 задаргааны 6-р гишүүнийг ол.
задаргааны 6-р гишүүнийг ол.