Алгебрын суурь ухагдхууны нэг бол илэрхийллийг хялбарчлах байдаг. Өмнөх хичээлээр рационал бутархай гэж юу болох тэдгээрийг хялбарчилахад үржүүлэхийн хураангуй томьёог хэрхэн ашиглахыг сайн ойлгоогүй бол Рационал бутархайтай ажиллаж сурах I хичээлийг үзэхийг зөвлөе. Бодлого бодох суурь аргачлал илэрхийллийн хялбарчлал дээр тогтдог. Үүнийг сайн эзэмшээгүй үед ямарч бодлого танд хүндрэл үүсгэх бүрэн боломжтой. Иймээс хичээлийг анхааралтай сайн судлан ойлгон авахыг хичээгээрэй.
Нэг үзээд ойлгохгүй бол дахиад үз. Хэн ч таныг олон удаа үзлээ гэхгүй. Интернет сургалтын хамгийн том давуу тал энэ. Зарим хичээлийг үзэхийн тулд багахан төлбөр төлөх хэрэгтэйг Бүртгүүлэх, тусгай эрх нээлгэх нийтлэлээс үзээрэй.
Материалыг тусгай эрхтэй хэрэглэгч үзнэ.
request_quoteТусгай эрх авах




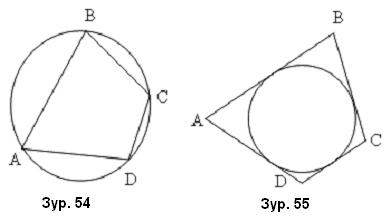
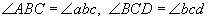 гэх мэт байна.
гэх мэт байна.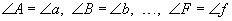 , харин талууд нь порпорционал байна.
, харин талууд нь порпорционал байна.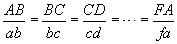
 илэрхийллийг хялбарчил.
илэрхийллийг хялбарчил.
 задаргааны 6-р гишүүнийг ол.
задаргааны 6-р гишүүнийг ол.