Логарифмын үндсэн томьёонууд. Илтгэгч ба логарифм тэгшитгэлүүдийг бодох зөвлөмж
Логарифмын үндсэн томьёонууд
| Дугаар | Тодорхойлолт | Томьёо |
| 5.1.1 | Үндсэн адилтгал | 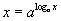 |
| 5.1.2 | Ижил суурьтай логарифм | 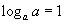 |
| 5.1.3 | Нэгийн логарифм | 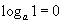 |
| 5.1.4 | Үржвэрийн логарифм | 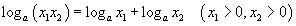 |
| 5.1.5 | Ногдворын логарифм | 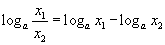 |
| 5.1.6 | Зэргийн логарифм | 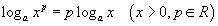 |
| 5.1.7 | Логарифмыг шинэ суурьт шилжүүлэх | 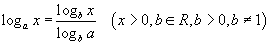 |
| 5.1.8 | 5.1.7 ийн тухайн тохиолдол | 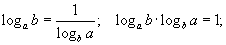 |
| 5.1.9 | 5.1.7 ийн тухайн тохиолдол | 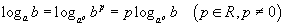 |
| 5.1.10 | Аравтын логарифм | 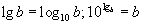 |
| 5.1.11 | Натурал логарифм | 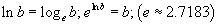 |
Илтгэгч ба логарифм тэгшитгэлүүдийг бодох зөвлөмж
5.2.1
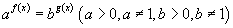 илтгэгч тэгшитгэлийг ямар нэгэн c≥0, c≠0 сууриар логарифмчилж
илтгэгч тэгшитгэлийг ямар нэгэн c≥0, c≠0 сууриар логарифмчилж 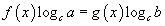 тэгшитгэлд шилжүүлнэ. Тухайлбал
тэгшитгэлд шилжүүлнэ. Тухайлбал 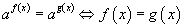
5.2.2
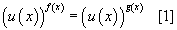 тэгшитгэлийн шийдээр зөвхөн
тэгшитгэлийн шийдээр зөвхөн 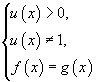 гэсэн холимог системийн шийд ба u(x)=1 байлгах, f(x),g(x) тодорхойлогдох x ийн утгыг тооцно.
гэсэн холимог системийн шийд ба u(x)=1 байлгах, f(x),g(x) тодорхойлогдох x ийн утгыг тооцно. 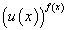 төрлийн функц нь зөвхөн u(x)≥0 үед тодрохойлогдох тул [1] тэнцлийг хангах x ийн утгыг тэгшитгэлийн шийдээр тооцно. u(x)≤0 байх x ийн утгыг тэгшитгэлийн шийдээр тооцохгүй.
төрлийн функц нь зөвхөн u(x)≥0 үед тодрохойлогдох тул [1] тэнцлийг хангах x ийн утгыг тэгшитгэлийн шийдээр тооцно. u(x)≤0 байх x ийн утгыг тэгшитгэлийн шийдээр тооцохгүй.
5.2.3
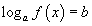 логарифм тэгшитгэл нь
логарифм тэгшитгэл нь 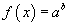 тэгшитгэлтэй эн чацуу
тэгшитгэлтэй эн чацуу
5.2.4
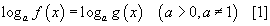 логарифм тэгшитгэл нь
логарифм тэгшитгэл нь 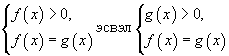 системүүдтэй эн чацуу. [1] тэгшитгэлийг бодохдоо дээрх хоёр системийн зөвхөн аль нэгийн нь эсвэл f(x)=g(x) тэгшитгэлийг бодно. Тэгшитгэл нь анхны тэгшитгэлийн хувьд гадны шийдтэй байж болох учраас шийдүүдийг анхны тэгшитгэлд орлуулж шалгана.
системүүдтэй эн чацуу. [1] тэгшитгэлийг бодохдоо дээрх хоёр системийн зөвхөн аль нэгийн нь эсвэл f(x)=g(x) тэгшитгэлийг бодно. Тэгшитгэл нь анхны тэгшитгэлийн хувьд гадны шийдтэй байж болох учраас шийдүүдийг анхны тэгшитгэлд орлуулж шалгана.
5.2.5
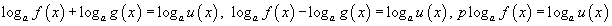 тэгшитгэлүүдийг бодохдоо 5.1.4 – 5.1.6 томьёонуудыг ашиглан
тэгшитгэлүүдийг бодохдоо 5.1.4 – 5.1.6 томьёонуудыг ашиглан 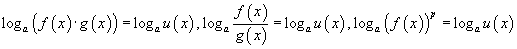 хэлбэрүүдэд шилжүүлээд дараа нь 5.2.4 зөвлөмжийн дагуу бодно. Олдсон шийдүүдээс f(x)≥0, g(x)≥0, u(x)≥0 байлгах эсвэл анхны тэгшитгэлд орлуулах аргаар тэгшитгэлийн шийдийг гаргана.
хэлбэрүүдэд шилжүүлээд дараа нь 5.2.4 зөвлөмжийн дагуу бодно. Олдсон шийдүүдээс f(x)≥0, g(x)≥0, u(x)≥0 байлгах эсвэл анхны тэгшитгэлд орлуулах аргаар тэгшитгэлийн шийдийг гаргана.
5.2.6
Тэгшитгэлийг 5.1.4 – 5.1.6 томьёонуудыг ашиглан хувиргалт хийх үед өгөгдсөн тэгшитгэлийн шийд алдагдах гэм бий. Ийм алдаа гаргахгүйн тулд томьёонуудыг дараах байдлаар ашиглах хэрэгтэй.
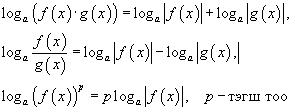





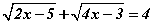 тэгшитгэл бод.
тэгшитгэл бод.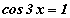 тэгшитгэл бод.
тэгшитгэл бод.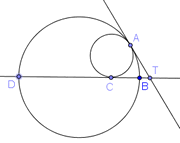 Зурагт өгөгдсөн дотоод байдлаараа шүргэлцсэн хоёр тойргийн TA нь ерөнхий шүргэгч, TC нь том тойргийн огтлогч, жижиг тойргийн шүргэгч болно. DC=3, CB=2 бол TA -г ол.
Зурагт өгөгдсөн дотоод байдлаараа шүргэлцсэн хоёр тойргийн TA нь ерөнхий шүргэгч, TC нь том тойргийн огтлогч, жижиг тойргийн шүргэгч болно. DC=3, CB=2 бол TA -г ол.