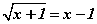 тэгшитгэлийн шийдийг ол.
тэгшитгэлийн шийдийг ол.
Бодолт
Иррационал тэгшитгэлийг бодохдоо тэгшитгэлийн тодорхойлогдох мужийг заавал тооцож байгаарай. Үүнийг тооцохгүйгээр бодолтыг хийн гадны шийдийг тэгшитгэлийн шийдээр тооцон алдаа хийх нь элбэг байдаг. Энэ талаар Иррационал тэгшитгэлийг бодох хичээлээс үзээрэй. Тэгшитгэлийг олон аргаар бодож болно.
Хамгийн энгийн бөгөөд ойлгомжтой арга бол эхлээд тэгшитгэлийн тодорхойлогдох мужийг олоод дараа нь тэгшитгэлийн шийдүүд тодорхойлогдох мужид орж байгааг шалгах байдаг. Иррационал тэгшитгэлийг бодохдоо
- Тэгш зэрэгтэй язгуур доорх илэрхийлэл тэгээс их буюу тэнцүү байх
- Тэгш зэргийн язгуур зөвхөн сөрөг биш утгыг авч болно
гэсэн хязгаарлалтыг санаж байх хэрэгтэй. Эдгээр хязгаарлалтыг тооцоод өгөгдсөн тэгшитгэлийн тодорхойлогдох мужийг олбол 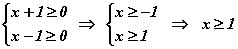 гэж гарна. Системийн эхний тэнцэтгэл биш бол эхний хязгаарлалт харин хоёрдугаар тэнцэтгэл биш бол хоёрдахь хязгаарлалт. Тэгшитгэлийн баруун талыг квадрат язгуурын шийд гэж үзнэ. Үүнийг сайн ойлгон аваарай. Одоо тэгшитгэлийн хоёр талыг квадрат зэрэг дэвшүүлбэл
гэж гарна. Системийн эхний тэнцэтгэл биш бол эхний хязгаарлалт харин хоёрдугаар тэнцэтгэл биш бол хоёрдахь хязгаарлалт. Тэгшитгэлийн баруун талыг квадрат язгуурын шийд гэж үзнэ. Үүнийг сайн ойлгон аваарай. Одоо тэгшитгэлийн хоёр талыг квадрат зэрэг дэвшүүлбэл 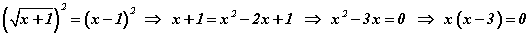 тэгшитгэл гарах бөгөөд эндээс
тэгшитгэл гарах бөгөөд эндээс 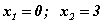 шийдүүд гарна. x=0 нь тодорхойлогдох мужид орохгүй тул тэгшитгэлийн шийд x=3 болно.
шийдүүд гарна. x=0 нь тодорхойлогдох мужид орохгүй тул тэгшитгэлийн шийд x=3 болно. 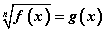 хэлбэрийн тэгшитгэлийн язгуурын зэрэг n тэгш байвал язгуурыг арифметикийн гэж үздэг учраас тодорхойлогдох мужийг тооцох шаардлагатай болдог тул тэгшитгэл
хэлбэрийн тэгшитгэлийн язгуурын зэрэг n тэгш байвал язгуурыг арифметикийн гэж үздэг учраас тодорхойлогдох мужийг тооцох шаардлагатай болдог тул тэгшитгэл 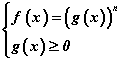 системтэй эн чацуу гэж үздэг. f(x)≥0 нөхцөл эхний тэгшитгэлд багтсан байгаа болохоор түүнийг тооцдоггүй. Энэ аргаар өгөгдсөн тэгшитгэлийг бодвол
системтэй эн чацуу гэж үздэг. f(x)≥0 нөхцөл эхний тэгшитгэлд багтсан байгаа болохоор түүнийг тооцдоггүй. Энэ аргаар өгөгдсөн тэгшитгэлийг бодвол 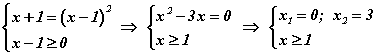 гээд бас x=3 болно.
гээд бас x=3 болно.
Өөр нэгэн арга бол тэгшитгэлийн хоёр талыг шууд квадрат зэрэг дэвшүүлэн бодоод 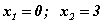 шийдүүдийг олоод тэдгээрийг анхдагч тэгшитгэлд орлуулан шалгавал
шийдүүдийг олоод тэдгээрийг анхдагч тэгшитгэлд орлуулан шалгавал 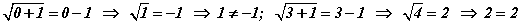 болсноор x=3 шийд гэдэг нь харагдана. Энд тэгш зэргийн язгуур зөвхөн сөрөг биш утгыг авна гэсэн хязгаарлалт үйлчилнэ.
болсноор x=3 шийд гэдэг нь харагдана. Энд тэгш зэргийн язгуур зөвхөн сөрөг биш утгыг авна гэсэн хязгаарлалт үйлчилнэ.
Аль ч аргыг ашиглан бодолтыг хийж болох ч би эхний аргыг хамгийн энгийн бөгөөд ойлгомжтой нь гэж зөвлөх байна.
Хариу
3





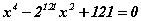 тэгшитгэлийн өөр өөр шийдүүд бол
тэгшитгэлийн өөр өөр шийдүүд бол 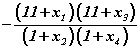 илэрхийллийн утгыг ол.
илэрхийллийн утгыг ол.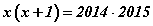 тэгшитгэлийг бод.
тэгшитгэлийг бод.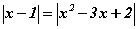 тэгшитгэлийг бод.
тэгшитгэлийг бод.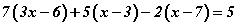 тэгшитгэлийг бод.
тэгшитгэлийг бод. функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол. тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.