Язгуур доор үл мэдэгдэгчийг агуулсан тэгшитгэлийг иррационал тэгшитгэл гэдэг. Ийм төрлийн тэгшитгэлийг бодохдоо тэгшитгэлд байгаа язгуурууд арифметикийн байх ёстой гэсэн нөхцлийг тооцон үл мэдэгдэгчийн утгын мужийг заавал тооцох хэрэгтэй. Үүнийг тооцоогүйгээс ихэнх алдаанууд гардаг. Хичээлээр иррационал тэгшитгэлийг бодох аргуудын талаар авч үзэх болно.
Сонгох арга.
Арга нь хэрвээ y=f(x) функц тодорхойлогдох муждаа өсөж байхад a тоо түүний утгын мужид харьяалагдаж байвал тэгшитгэл f(x)=a гэсэн цорын ганц шийдтэй байна гэсэн онолын ухагдхуун дээр үндэслэнэ. Энэхүү баталгааг үндэс болгосон аргыг ашиглахдаа
- Тэгшитгэлд байгаа функцуудыг ялган авна
- Функцуудын тодорхойлогдох мужуудыг олно
- Тодорхойлогдох муждаа функцууд монотон гэдгийг батална
- Тэгшитгэлийн язгуурыг сонгоно
- Өөр шийдгүй гэдгийг баталгаажуулна
- Хариугаа бичнэ
Энэ аргаар бодогдох тэгшитгэлүүд дээр бага ажилладагаас аргыг хэрэглэхдээ сурагчид тааруухан байдаг. Өөрөөр хэлбэл ойлголт дутуу гэсэн үг. Арга нь их энгийн болоод үр дүнтэй гэдгийг доорх жишээнүүд батална.
Бодлого 3.053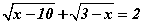 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Бодолт
Бодлого 3.054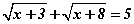 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Бодолт
Тэгшитгэлийн хоёр талыг ижил зэрэг дэвшүүлэх арга.
Хэрвээ f(x)=g(x) [1] тэгшитгэлийн хоёр талыг n натурал тоон зэрэг дэвшүүлбэл fn(x)=gn(x) [2] тэгшитгэл нь [1] тэгшитгэлийн мөрдлөг болно.
Баталгаа. Хэрвээ f(a)=g(a) гэсэн тоон тэнцэл биелэгдэж байвал зэргийн чанараар fn(a)=gn(a) тэнцэл биелэгдэнэ. Өөрөөр хэлбэл [1] тэгшитгэлийн шийдүүд [2] тэгшитгэлийн шийд мөн. Энэ нь [2] тэгшитгэл нь [1] тэгшитгэлийн мөрдлөг гэдгийг харуулна.
Хэрвээ n=2k+1 /сондгой/ бол эсрэг теорем хүчинтэй. Энэ тохиолдолд [1], [2] тэгшитгэлүүд эн чацуу.
Хэрвээ n=2k /тэгш/ бол f(x)=g(x) ба f(x)=-g(x) тэнцлүүдийн аль нэг нь биелэгдэж байвал f2n(a)=g2n(a) тэнцэл биелэгдэнэ. Энэ тохиолдолд [1], [2] тэгшитгэлүүд эн чацуу биш гэсэн үг. Иймээс f(x)=g(x) иррационал тэгшитгэлийн бодолтыг хийх үед түүний хоёр талыг тэгш зэрэг дэвшүүлэхээр болбол гадны шийд бий болох талтай. Шалгалтаар гадны шийдээс салахын оронд g(x)≥0 гэсэн нэмэлт нөхцлийг оруулан өгнө. Тэгвэл 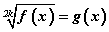 тэгшитгэл
тэгшитгэл 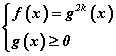 системтэй эн чацуу болно. Системд 2k зэргийн язгуурын шийдийг хангах f(x)≥0 нөхцөл байхгүй байгаа. Энэ нь f(x)=g2k(x) тэнцэл байгаа учраас илүүц юм.
системтэй эн чацуу болно. Системд 2k зэргийн язгуурын шийдийг хангах f(x)≥0 нөхцөл байхгүй байгаа. Энэ нь f(x)=g2k(x) тэнцэл байгаа учраас илүүц юм.
Иррационал тэгшитгэлийг бодоход энэ аргыг хамгийн ихээр ашигладаг. Харин сурагчид сүүлийн нэмэлт нөхцлийг орхигдуулан бодсноос гадны шийдийг шийдэд оруулан алдаа гаргах нь маш элбэг байдаг. Аргыг ашиглахыг жишээн дээр харцгаая.
Бодлого 3.055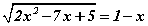 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Бодолт
Хэрвээ тэгшитгэлд олон язгуурууд орсон байвал ээлж дараалан зэрэг дэвшүүлэх аргаар тэдгээрээс салах хэрэгтэй. Ингэхдээ анхны тэгшитгэлийн тодорхойлогдох мужийг тооцсон байх хэрэгтэй.
Бодлого 3.056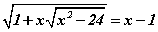 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Бодолт
Зарим тэгшитгэлийн тодорхойлогдох мужийг тооцоход төвөгтэй байвал бодолтыг хийгээд шийдийг олоод анхдагч тэгшитгэлд шууд оруулан шалгаж бас болно.
Бодлого 3.057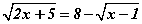 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Бодолт
Шинээр хувьсагч оруулах арга
Зарим тохиолдолд шинэ хувьсагч оруулах нь тэгшитгэлийг хураангуй хэлбэрт оруулснаар бодолтыг хялбар болгодог. Шинэ хувьсагчаар ихэнхдээ тэгшитгэлийн язгууртай гишүүнийг авдаг. Ингэхэд тэгшитгэл шинээр оруулсан хувьсагчаас хамаарсан тэгшитгэл болон хувирна. Энэ аргыг бас орлуулах арга ч гэж нэрлэх бөгөөд бүх төрлийн тэгшитгэлийг бодоход өргөнөөр ашигладаг.
Бодлого 3.058 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Бодолт
Аргуудыг хэрэглэхийн өмнө анхдагч тэгшитгэлд тодорхой хувиргалтыг хийх тохиолдол байдаг. Доор үзүүлсэн жишээнд нилээд нарийн хувиргалтыг хийгээд дараа нь орлуулга хийж байгаад анхаарна уу. Ийм төрлийн хувиргалтыг ямарч төрлийн тэгшитгэлд хийж сурах хэрэгтэй.
Бодлого 3.059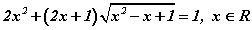 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Бодолт
Тэгшитгэлийн илэрхийллийг үржигдхүүнд задлах арга.
Бүх тоон тэнхлэгт тодорхойлогдох f(x)·g(x)=0 тэгшитгэл нь 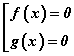 гэсэн тэгшитгэлүүдийн багцтай эн чацуу гэсэн теорем дээр үндэслэсэн арга. Теоремийг ямарч төрлийн тэгшитгэлийг бодоход ашигладаг. Илэрхийллийг үржигдхүүнд задлах аргуудын талаар Бодлого бодож сурах цуврал хичээлүүдээс үзээрэй.
гэсэн тэгшитгэлүүдийн багцтай эн чацуу гэсэн теорем дээр үндэслэсэн арга. Теоремийг ямарч төрлийн тэгшитгэлийг бодоход ашигладаг. Илэрхийллийг үржигдхүүнд задлах аргуудын талаар Бодлого бодож сурах цуврал хичээлүүдээс үзээрэй.
Бодлого 3.060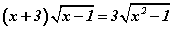 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Бодолт
Зарим үед ерөнхий үржигдхүүнийг олох нь маш хүнд байдаг. Ийм тохиолдолд нэмэлт хувиргалт хийсний дараа л үржигдхүүнд задлах боломж гарч ирдэг. Үүнийг доорх жишээ батална.
Бодлого 3.061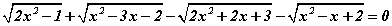 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Бодолт
Бүтэн квадрат ялгах арга.
Зарим нэгэн тэгшитгэлийг бодоход 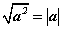 томьёо хэрэг болдог. Энэ нь тэгшитгэлийн язгуур доорх илэрхийллийг бүтэн квадрат хэлбэрт оруулаад язгуур нь тухайн илэрхийллийн модултай тэнцүү байдаг чанарыг ашиглах санаа юм.
томьёо хэрэг болдог. Энэ нь тэгшитгэлийн язгуур доорх илэрхийллийг бүтэн квадрат хэлбэрт оруулаад язгуур нь тухайн илэрхийллийн модултай тэнцүү байдаг чанарыг ашиглах санаа юм.
Бодлого 3.062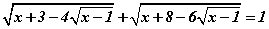 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Бодолт
Үнэлгээний арга
Энэ аргыг тэгшитгэлийн язгуур доорх илэрхийлэл үржигдхүүнд задрахгүй гурван гишүүнт хэлбэрийн байхад ашигладаг. Иймээс тэгшитгэлийн зүүн ба баруун хэсэгт үнэлгээ өгөх шаардлага гарна.
Бодлого 3.063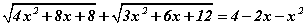 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Бодолт
Хоёрдугаар эрэмбээс дээш зэрэг агуулсан иррационал тэгшитгэл
Хэрвээ тэгшитгэл 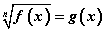 хэлбэртэй байвал тэнцүүгийн тэмдгийн хоёр талыг n зэрэг дэвшүүлэн бодолтыг хийнэ. Зэрэг дэвшүүлснээр гарах тэгшитгэл нь сондгой n -ийн хувьд
хэлбэртэй байвал тэнцүүгийн тэмдгийн хоёр талыг n зэрэг дэвшүүлэн бодолтыг хийнэ. Зэрэг дэвшүүлснээр гарах тэгшитгэл нь сондгой n -ийн хувьд 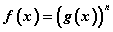 тэгшитгэлтэй энэ чацуу байх ба харин тэгш n -ийн хувьд бидний авч үзсэн n=2 ижилхэн байна.
тэгшитгэлтэй энэ чацуу байх ба харин тэгш n -ийн хувьд бидний авч үзсэн n=2 ижилхэн байна.
Бодлого 3.064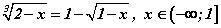 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Бодолт
Иррационал тэгшитгэлийг бодоход дараах аргыг ихээр ашигладаг. Хэрвээ a+b=c бол a3+3ab(a+b)+b3=c3 байна. Энэ бол нийлбэрийн кубын томьёо. Харин сүүлийн тэнцэлд (a+b) -г c -гээр соливол 3abc=c3-b3-a3 болох бөгөөд цааш хоёр талыг куб зэрэг дэвшүүлэн иррационалаас амархан салах юм. Үүнийг жишээн дээр авч үзье.
Бодлого 3.065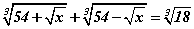 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Бодолт
Тайлбар. Бодлогын зүүн хэсэгт баруун хэсгээр нь орлуулга хийх нь ерөнхий тохиолдолд зөвтгөх үйлдэл биш. Учир нь бидэнд тэгшитгэлийг зөв тоон тэнцэл болгох x -ийн ямар ч утга мэдэгдэхгүй байгаа шүү дээ. Ийм шийд байхгүй ч байж мэднэ. Бодлого бодохдоо ийм орлуулга хийснээр бид үнэн хэрэгтээ боломжит шийдийн олонлогийг өргөтгөж байгаа юм. Иймээс олдсон бүх шийдийг шалган тэгшитгэлийг зөв тоон тэнцэл болгох шийдүүдийг хариугаар сонгох хэрэгтэй.
Олон бодлого бодсноор чадвар дээшлээд байна гэвэл өрөөсгөл. Сургалтын үр өгөөж уншсан, судалсан зүйлийн хэмжээгээр биш түүнийг хэрхэн эзэмшсэн байдлаар дүгнэгдэнэ. Иймд сайтын хичээлүүдийг үзэн бодлогуудын жишээтэй танилцаж байхдаа тухайн бодлогыг олон аргаар бодохыг байнга оролдож байгаарай. Энэ нь таны сэтгэлгээг маш идэвхитэй хөгжүүлэх сайн арга гэдгийг санаж байгаарай. Бодлогыг олон аргаар хэрхэн бодох жишээг үзэцгээе.
Бодлого 3.066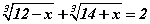 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Бодолт
Бодлогыг заавал энэ тэр аргаар бодно гэсэн дүрэм байхгүй гэдгийг дээрх жишээ баталж байна. Гэхдээ тодорхой хэлбэрийн бодлогуудыг таарах аргаар нь бодох нь илүү хурдан бөгөөд үр дүнтэй.





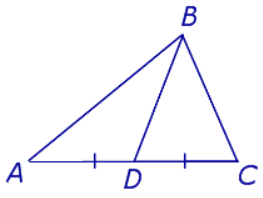
 задаргааны хамгийн их нэмэгдхүүн
задаргааны хамгийн их нэмэгдхүүн  бол a, b, c -г ол.
бол a, b, c -г ол. тэгшитгэлийг бод.
тэгшитгэлийг бод. функцийн уламжлалын
функцийн уламжлалын  утгыг ол.
утгыг ол.