Бодлого бодохыг юу гэж ойлгох вэ? Бидний ихэнх нь бодлогыг ухаантай хүмүүс л боддог гэж ойлгоод байдаг. Математикийн шинжлэх ухаанд шийдэгдээгүй асуудлууд олон бий. Эдгээрийн шийдлийг гарган теорем, дүрэм батлах зэрэг нь үнэхээр ухаантай хүмүүсийг ажил. Энэ бол зөвхөн математикийн ухаанд ч биш бүхий л салбарт ийм жамтай. Харин эдгээр суут хүмүүсийн гаргасан шийдлийг хүн бүр өдөр тутмын амьдралдаа байнга ашиглаж байдгаа тэр бүр мэдээд байдаггүй. Жирийн хүмүүсийн хувьд математикийн бодлого бодно гэдэг нь ердөө эрдэмтэн мэргэдийн гаргасан шийдлийг ашиглах л юм. Түүнээс шинээр ямар нэгэн арга зохиогоод шийдэл гаргаад байх ерөөсөө биш. Бодлого бодох гэдэг нь компьютер ашиглах, гар утасны функцээ ажлуулах, машин жолоодохтой ижил ердийн ажил.

Илүү юу ч байхгүй. Эдгээрт үндсэн бөгөөд ерөнхий нэг зүйл бол тодорхой дүрмийг л зөв баримтлах л юм. Жишээ нь та машин жолоодож яваад зогсохын тулд хурдаа хасахаас эхлээд зогсоох дарааллыг баримтлах ёстой. Түүнээс улам хааз өгөөд байвал машин зогсохгүй нь ойлгомтой. Бодлого бодох нь үүнтэй яг адилхан. Бодлогод байгаа тоонуудыг ямар ч дүрэмгүйгээр хооронд нь хасах, нэмэх гээд төрөл бүрийн үйлдлийг хийгээд байж болохгүй. Тэгвэл бодлого бодогдохгүй гэсэн үг.

Ямарч бодлогын шийдлийг олохын тулд та математик модел буюу илэрхийлэлд адитгал хувиргалтыг шат дараалан хийн энгийн хэлбэрт оруулаад тодорхой томьёонуудыг ашиглан хариу гаргах л байдаг. Эндээс бодлого бодох үндсэн суурь бол илэрхийлэлд адитгал хувиргалт хийж сурах юм. Илэрхийлэл,  адитгал хувиргалтын талаар бид Илэрхийллийг хялбарчлах хичээлд үзсэн.
Илэрхийллийг энгийн хэлбэрт оруулах үндсэн арга бол түүнийг үржигдхүүнд задлах. Үржигдхүүнд задлана гэдэг нь илэрхийллийг хэд хэдэн илэрхийллүүдийнн үржвэр хэлбэрт оруулахыг хэлнэ.
Жишээ нь 12 -г үржигдхүүнд задал гэвэл 12=2·6 гээд бичиж болно. Хэдийгээр тэнцүүгийн тэмдгийн хоёр талын илэрхийллийн хэлбэр өөр боловч 2·6 нь 12 гэдгийг бид бүгд мэднэ. Энд гол нь хувиргалтаар 12 тооны утга өөрчлөгдөхгүй байх л ёстой. Үүнээс гадна 12 -г 12=3·4=2·2·3=1·12=0,6·20 ... гэх мэтээр төгсгөлгүй олон хэлбэрээр хувиргах боломжтой. Тоог үржигдхүүнд задлаж сурах нь язгуурын үйлдэлд маш хэрэг болно.
Алгебрын илэрхийллийг үржигдхүүнд задлах ашигтайгаас гадна бүр хэрэгтэй зүйл шүү. Жишээ нь 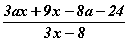илэрхийллийг хялбарчил. Илэрхийллийг хялбарчилж чаддаг бол та a+3 илэрхийллийг гаргах болно. Ингээд илэрхийллийг үржигдхүүнд задлах аргуудтай танилцая.

Үржигдхүүнд задлах үндсэн аргууд

Илэрхийллийг үржигдхүүнд задлах олон аргууд байдгаас хамгийн өргөн хэрэглэдэг аргуудад

• Ерөнхий үржигдхүүнийг хаалтнаас гаргах
• Бүлэглэх
• Үржүүлэхийн хураангуй томьёог ашиглах
• Квадрат гурван гишүүнтийг үржвэрт задлах
• Олон гишүүнтийг хоёр гишүүнтэд хуваах

аргууд ордог. Дээрх аргуудыг яг дарааллаар нь цээжлээрэй. Төвөгтэй илэрхийллүүдийг эмхэтгэхийн тулд бүхий л боломжит аргуудаар шалгах хэрэгтэй. Гэхдээ дээр өгсөн дарааллын дагуу шалгах нь илүү. Эдгээр аргуудыг мэддэг байхад алгебрын илэрхийллүүдийн ихэнхийг эмхэтгэх боломжтой.  

Ерөнхий үржигдхүүнийг хаалтнаас гаргах

Энгийн бөгөөд хэрэгтэй арга. a(b+c)=ab+ac гэдгийг бүгд мэднэ. Илүү ерөнхий байдлаар өгвөл a(b+c+d+...)=ab+ac+ad+... Эдгээр тэнцлийг ab+ac=a(b+c) гээд бичиж болно. Эсхүл ab+ac+ad+...=a(b+c+d+...). Энэ бол ерөнхий үржигдхүүнийг хаалтнаас гаргах дүрмийн утга учир. Тэнцүүгийн тэмдгийн зүүн талд a - нь бүх нэмэгдхүүнүүдийг үржүүлж байгаа бол баруун талд a -г хаалтны өмнө гаргасан байгаа нь хаалтанд доторх бүх гишүүдийн хувьд ерөнхий үржигдхүүн гэдгийг зааж байгаа юм. Хаалтыг задалбал хаалтанд байгаа бүгдийг a -гаар үржүүлснээр зүүн тал гараад ирэх болно.
Аргыг хэрхэн ашиглахыг маш энгийн жишээн дээр авч үзье.
Жишээ 1
ax+9x илэрхийллийг үржигдхүүнд задал
Бодолт
Нэмэгдхүүнүүдэд ямар ерөнхий үржигдхүүн байгааг харъя. Мэдээжээр энэ бол x. Тэгвэл x-ийг хаалтны өмнө гаргая. Үүнийг хийхдээ x - ийг бичээд хаалтаа нээнэ. Хаалтанд илэрхийллийн бүх гишүүдийг ерөнхий үржигдхүүнд хуваахад гарах үр дүнг бичин өгнө.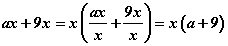
ингээд гүйцээ. Бодит байдалд ийм дэлгэрэнгүй бичээд байх албагүй. Хуваах үйлдлийг цээжээр хийгээд явдаг. Эхний ээлжинд дадалтай болтлоо ийм маягаар хийгээд байж болох юм. Эндээс ерөнхий үржигдхүүнийг хаалтны өмнө гаргах эхний дүрэм бол

• Ерөнхий үржигдхүүнийг хаалтны өмнө бичнэ.
• Хаалтанд илэрхийллийн бүх гишүүдийг хаалтын өмнө гаргасан ерөнхий үржигдхүүнд хуваан гарсан үр дүнг илэрхийлэлд байгаа дарааллын дагуу бичин өгнө.

Энэ дүрмийг тогтоогоод аваарай.
Бид ax+9x илэрхийллийг үржигдхүүнд задлан x(a+9) хэлбэртэй болголоо. Анхдагч илэрхийлэлд үржвэр байсан. Гэхдээ бүр a·x, 9·x гэсэн хоёр үржвэр байсан. Энэ хоёр үржвэр байгаагүй бол илэрхийлэл үржигдхүүнд задрахгүй байсныг тэмдэглэе. Үүнээс гадна анхдагч илэрхийлэлд бас +  үйлдэл байсан. Харин x(a+9) илэрхийлэлд үржвэрээс өөр үйлдэл байхгүй болсон. Хаалтанд байгаа + тэмдэг юу вэ? гэж асууж болно. Хаалтанд нэмэх үйлдэл бий. Гэхдээ хаалтыг задлаагүй байхад бид хаалтан доторхийг нэг үсгээр xb гэж үзэж болно. Энэ утгаараа x(a+9) илэрхийлэлд үржвэрээс өөр үйлдэл байхгүй гэж үзэх боломжтой. Энд л үржигдхүүнд задлахын утга оршиж байгаа юм.
Үржигдхүүнд задлахдаа бүгдийг зөв хийсэн эсэхээ шалгах боломжтой юу? Энэ амархан. Ерөнхий үржигдхүүнээр хаалтанд байгаа илэрхийллийг гишүүнчлэн үржүүлээд анхны илэрхийлэл гарч буйг шалгана. Үүнийг хаалтыг задлах гэж нэрлэдэг. Эндээс дараагийн дүрэм бол

Шаардлагатай бол буцаан үржүүлэх /хаалтыг задлах/ замаар зөв задалсан эсэхээ шалгаж болно.

Жишээ 2  
3ax+9x илэрхийллийг үржигдхүүнд задал
Бодолт
Ерөнхий үржигдхүүн байна уу. Байна аа. x бүгдэд байгаа учраас ойлгомжтой. Дахиад ерөнхий үржигдхүүн байна уу. Илэрхийллийг 3ax+3·3x хэлбэрээр бичвэл 3 гэсэн дахин нэг ерөнхий үржигдхүүн байгаа нь харагдана. Энд ерөнхий үржигдхүүнийг шууд 3x гэж үзээд хаалтны өмнө гаргавал 3ax+3·3x=3x(a+3) болон задарна.
Эндээс дахин нэг мөрдлөг гарна.

Ерөнхий үржигдхүүнийг хаалтны өмнө гаргахдаа хамгийн ихийг нь сонгохыг хичээх хэрэгтэй.

Дахин нэг жишээ аваад үзье.
3ax+9x-8x-24 илэрхийллийг үржвэрт задал.
Юуг хаалтны өмнө гаргах вэ? 3 -г эсхүл x -ийг үү. Болохгүй. Илэрхийллийн бүх гишүүнд байгаа ерөнхий үржигдхүүнийг л зөвхөн хаалтны өмнө гаргаж болдог гэдгийг дахин сануулъя. Гэтэл тийм ерөнхий зүйл энэ илэрхийлэлд алга. Тэгвэл яахыг дараагийн Бүлэглэх аргаас харцгаая.