Арифметикт суралцаж буй сурагчид арифметикийн үндсэн дөрвөн үйлдлийн дүрэм болоод үйлдлүүдийг оновчтой хурдан хийх аргыг маш сайн эзэмших хэрэгтэй. Эдгээр дүрэм, аргачлалууд алгебрийн илэрхийллийн хувиргалтуудын суурь болдог гэдгийг санаарай. Дүрмүүд энгийн тул сурагчид болон эцэг эхчүүд нэг их анхаарахгүй өнгөрөөснөөс болоод алгебр орж эхлэхэд суурь дүрмүүдээ мэдэхгүйгээс үүдэн хоцрогдол үүсэх цаашлаад математикийн хичээлд дургүй болох шалтгаан ч болох эрсдэлтэй.
Нийлбэрийг тоогоор, тоог нийлбэрээр үржих үйлдлийг хоёр аргаар хийж болно.
1-р арга. Эхлээд нийлбэрийг олоод гарсан үр дүнг тоогоор үржүүлнэ.
Жишээ нь (4 + 5) · 3 илэрхийллийн утгыг ол. Аргын дагуу эхлээд хаалтанд доторх 4 ба 5 -ын нийлбэрийг олвол 4 + 5 = 9 гарна. Одоо үр дүнг 3 -аар үржүүлбэл 9 · 3 = 27 гарна. (4 + 5) · 3 = 9 · 3 = 27 гэсэн үг.
2-р арга. Нийлбэрийн бүрдүүлэгч бүрийг тухайн тоогоор үржүүлээд гарсан үр дүнгүүдийг нэмэж болно.
(4 + 5) · 3 илэрхийллийн утгыг олох жишээг авч үзье. Аргын дагуу нийлбэрийн бүрдүүлэгч бүрийг тухайн тоогоор үржүүлбэл 4 · 3 = 12; 5 · 3 = 15 болно. Гарсан үр дүнгүүдийн нийлбэрийг олбол 12 + 15 = 27 гэж гарна. Үйлдлийг нэг мөрөөр хийвэл (4 + 5) · 3 = 4 · 3 + 5 · 3 = 27 гэсэн үг.
Нийлбэрийг тоогоор, тоог нийлбэрээр үржих үйлдлийг
(a + b) · c = a · c + b · c
ерөнхий томьёогоор илэрхийлж болно. Энэ томьёо нь үржвэрийн гишүүнчлэн үржүүлэх дүрэм юм.
Аргуудыг үржүүлэх үйлдлийг амархан гүйцэтгэхэд ашиглах боломтой.
Жишээ
(4 + 6) · 5; (4 + 3) · 5 илэрхийллүүдийн утгыг ол.
Бодолт
Эхний илэрхийллийн утгыг 1-р аргаар (4 + 6) · 5 = 10 · 5 = 50 харин хоёрдахь илэрхийллийн утгыг 2-р аргаар (4 + 3) · 5 = 4 · 5 + 3 · 5 = 20 + 15 = 35 гэж олох нь амар.
Нийлбэрийг тоогоор, тоог нийлбэрээр үржих үйлдлийг хийхдээ
- Нийлбэр бүхэл үр дүн өгөхөөр бол 1-р аргыг
- Нийлбэрийн бүрдүүлэгч бүрийг тоогоор үржүүлэхэд бүхэл үр дүн өгөхөөр бол 2-р аргыг
ашиглавал илүү хурдан алдаагүй тооцох боломжтой.
Үржвэрийн гишүүнчлэн үржүүлэх дүрмийг хоёр оронтой тоог нэг оронтой тоогоор үржүүлэх үйлдэлд хэрэглэх боломжтой.
Хоёр оронтой тоог нэг оронтой тоогоор үржүүлэхдээ хоёр оронтой тоог оронгийн бүрдүүлэгчээр нь салган нийлбэр болгоод нийлбэрийг нэг оронтой тоог үржүүлнэ.
Жишээ нь 32 · 5 илэрхийллийн утгыг олохын тулд эхлээд 32 -ийг оронгийн бүрдүүлэгчээр нь задлан 30 + 2 нийлбэр болгоно. Өөрөөр хэлбэл 3 аравт, 2 нэгжийн нийлбэр болгоно. Дараа нь 30 + 2 нийлбэрийг 5 -аар үржүүлэх буюу (30 + 2) · 5 үржвэрийг олно. Гишүүнчлэн үржүүлэх дүрмээр (30 + 2) · 5 = 30 · 5 + 2 · 5 = 150 + 10 = 160 гэж гарна.
Нэг оронтой тоог хоёр оронтой тоогоор үржүүлэх жишээ нь 3 · 24 тохиолдолд үржихийн байр солих дүрмээр үржигдхүүнүүдийн байрыг солиод 3 · 24 = 24 · 3 = (20 + 4) · 3 = 20 · 3 + 4 · 3 = 60 + 12 = 72 гэж тооцож болно. Эсхүл 3 · 24 = 3 · (20 + 4) = 3 · 20 + 3 · 4 = 60 + 12 = 72 гэсэн ч болно.





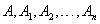 гэсэн төгсгөлөг цэгийн багц байна. Тэгвэл AB хэрчим дээр байгаа
гэсэн төгсгөлөг цэгийн багц байна. Тэгвэл AB хэрчим дээр байгаа 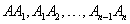 хэрчмүүд нь CD дээрх хэрчмүүдтэй тэнцүү бөгөөд A ба
хэрчмүүд нь CD дээрх хэрчмүүдтэй тэнцүү бөгөөд A ба 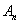 хооронд B цэг оршино.
хооронд B цэг оршино. функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол. тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.