Модул ухагдхууныг сурагчид бүгд мэддэг ч түүнийг сайн ойлгосон нь маш цөөн байдаг. Асуудлын гол нь модул сэдвийн хичээлийг өнгөцхөн үздэг дээр нь бодит амьдралд модул оролцсон жишээнүүд цөөн тохиолддогтой холбоотой байж мэднэ. Иймээс модултай тэгшитгэлийг хэрхэн бодох талаар авч үзье. Модул гэхээр сурагчид их хүнд хэцүү зүйл гээд зайлсхийх гээд байдаг ч үнэн хэрэгтээ тийм ч хүнд ойлголт ердөө биш гэдгийг хичээлийг үзээд мэднэ. Материалыг хөнгөн, ойлгоход амар байлгах үүднээс таслан оруулна. Хүүхдүүд олон хуудас материалыг судлан ойлгох нь хүндрэлтэй байж болох талтай. Материалыг 30-40 минутын хичээлийн конспект байдлаар бэлтгэн хүргэх нь илүү үр дүнтэй гэж үзсэн хэрэг.
Багахан онол
Эхлээд модул гэж юу вэ? гэдгээс эхлэе. Сөрөг тооны модул гэдэг нь сөрөг тэмдэггүй л тухайн тоо өөрөө гэдгийг сануулъя. Жишээ нь |-9|=9; |-120,68|=120,58; |-11|=11 гэх мэтээр.
Тэгвэл эерэг тооны модул юутай тэнцүү вэ? гэсэн асуулт гарч ирнэ. Энд асуудал бүр энгийн. Эерэг тооны модул гэдэг нь тухайн тоотойгоо тэнцүү. Жишээ нь |9|=9; |120,68|=120,58; |11|=11 гэх мэтээр.
Эндээс өөр тоонууд нэг ижил модултай байх сонин зүйл гарч ирэх нь. Жишээ нь |-9|=|9|=9; |-120,68|=|120,68|=120,58; |-11|=|11|=11 гэх мэтээр
Жишээнээс харилцан эсрэг тоонууд ижилхэн модултай гэдгийг амархан олж харна. Эндээс эсрэг тоонуудын модулууд тэнцүү гэдгийг тогтоогоод аваарай.
Дээрх жишээнүүдийг алгебрын бичлэгээр бичвэл
|−a|=|a|=a
гэсэн үг.
Бас нэг чухал зүйл бол модул хэзээ ч сөрөг байдаггүй. Эерэг ч бай сөрөг ч бай ямар нэгэн тооны модул үргэлж эерэг эсхүл дор хаяад тэгтэй тэнцүү. Ийм учраас модулийг тооны абсалют хэмжээ гэж ихэнхдээ нэрлэдэг.
Эерэг ба сөрөг тоонуудын модулийн тодорхойлолтыг нэгтгэвэл тооны модул гэдэг нь хэрвээ тоо эерэг байвал тухайн тоо өөрөө эсхүл тэг харин сөрөг байвал түүний эсрэг тоотой тэнцүү байдаг гэсэн бүх тооны модулийн суурь тодорхойлолт гарч ирнэ. Үүнийг томьёо хэлбэрээр
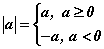
гэж бичнэ. Тэг нь эсрэг тоогүй цорын ганц тоо тул тэгийн модул нь тэг л байдаг.
y=|x| функцийн графикийг байгуулбал
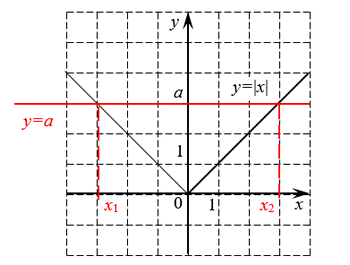
дээрх дүрс үүснэ. Зургаас |-m|=m гэдэг нь шууд харагдах ба модулийн график абсцисс тэнхлэгээс доош ордоггүй. Үүнээс гадна улаан шугамаар тэмдэглэсэн y=a шулуун a -гийн эерэг утганд x1, x2 гэсэн шийдийг өгч байгааг анхаарна уу. Энэ талаар сүүлд авч үзнэ.
Модулд алгебрын тодорхойлолтоос гадна геометрийн тодорхойлолт гэж бий. Тоон шулуун дээр x1, x2 цэгүүд байлаа гэе. Энэ тохиолдолд |x1- x2| илэрхийлэл нь эдгээр цэгүүдийн хоорондын зай эсхүл цэгүүдийг холбосон хэрчмийн урттай тэнцүү.
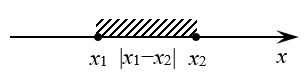
Модулийн геометр тодорхойлолтоор модул гэдэг нь тоон шулуун дээрх цэгүүдийн хоорондын зай. Цэгүүдийн хоорондын зай дандаа эерэг байх нь ойлгомжтой. Модулийн онолоос дээрх ойлголттой байхад хангалттай.
Үндсэн томьёонууд
Модулийн тодорхойлолтыг мэддэг байсан ч модул орсон тэгшитгэлийг бодоход амар болохгүй. Сурагчид модулийн тодорхойлолтыг мэдэж байгаа мөртлөө модултай тэгшитгэлийг ердөө бодож чадахгүй байх нь элбэг. Тэгэхлээр хамгийн энгийнээс эхлэн |x|=3 тэгшитгэлийг авч үзье.
x-ийн модул 3 -тай тэнцүү тэгшитгэлийн шийд ямар байх вэ? Тодорхойлолтоор |3|=3 байдаг болохоор x=3 тэгшитгэлийг бүрэн хангана. Тэгшитгэлийг хангах өөр тоо бий юу? Дахиад тодорхойлолтыг санавал |-3|=3 байдаг болохоор x=-3 тэгшитгэлийн шийд болно. Модул нь 3 тай тэнцүү байх өөр тоо байхгүй тул цааш өөр шийд хайх хэрэггүй. Эндээс |x|=3 тэгшитгэл x=3; x=-3 гэсэн шийдүүдтэй.
Одоо бодлогоо багахан хүндрүүлье. Модул доторх x -ийн оронд f(x) функцийг харин 3 -ын оронд дурын a тоог тавивал |f(x)|=a гэсэн тэгшитгэл үүснэ. f(x) функц, a дурын тоо гэдгээс тэгшитгэлүүдийг үүсгэвэл |2x+1|=5 эсхүл |10x-5|=-65 гээд хязгааргүй олон тэгшитгэлийг үүсгэж болно.
Модулийн тодорхойлолтоор тооны модул хэзээ ч сөрөг тоо байдаггүй гэдгээс |10x-5|=-65 тэгшитгэл шийдгүй гэдгийг шууд тогтооно. Харин |2x+1|=5 тэгшитгэлийн хувьд шийдийг хайх хэрэгтэй. Модул доторх илэрхийлэл эерэг эсхүл сөрөг байх хоёр тохиолдол бий. Хэрвээ илэрхийлэл эерэг буюу + тэмдэгтэй бол |2x+1|=2x+1 харин сөрөг байвал |2x+1|=-(2x+1)=-2x-1 гэж модулаас гарна. Сөрөг илэрхийллийг модулаас гаргаж байгааг сурагчид сайн ойлгодоггүй. Тодорхойлолтыг санавал сөрөг тооны модул өөрийн эсрэг тоотой тэнцүү гэдгээс -(2x+1) гарч байгаа юм. Тоог -1 -ээр үржүүлбэл тухайн тооныхоо эсрэг тоо болдог. Иймээс модул доторх 2x+1 илэрхийлэл сөрөг тэмдэгтэй бол түүнийг эсрэг тоо руу шилжүүлэхийн тулд -1 ээр л үржүүлэхэд хангалттай. Хаалтыг задалбал -2x-1 болно. 2x+1 илэрхийлэл эерэг тохиолдолд модул нь илэрхийлэлтэй тэнцүү байх тул тэгшитгэлийн 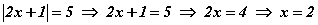 шийдийг төвөггүй олно. Харин 2x+1 илэрхийлэл сөрөг байвал
шийдийг төвөггүй олно. Харин 2x+1 илэрхийлэл сөрөг байвал 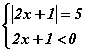 системийг бодох хэрэгтэй болно. Яагаад систем үүссэнг тайлбарлая. Эхний тэгшитгэлийн шийд илэрхийллийг сөрөг утгатай байлгах нөхцлийг хангаж байвал анхдагч тэгшитгэлийн нэг шийд болж чадах учраас 2x+1 илэрхийлэл сөрөг буюу тэгээс бага нөхцлийг давхар авч үзэж байгаа юм. 2x+1 илэрхийлэл сөрөг тэмдэгтэй үед модулаас хэрхэн гарахыг мэдэх тул системийг
системийг бодох хэрэгтэй болно. Яагаад систем үүссэнг тайлбарлая. Эхний тэгшитгэлийн шийд илэрхийллийг сөрөг утгатай байлгах нөхцлийг хангаж байвал анхдагч тэгшитгэлийн нэг шийд болж чадах учраас 2x+1 илэрхийлэл сөрөг буюу тэгээс бага нөхцлийг давхар авч үзэж байгаа юм. 2x+1 илэрхийлэл сөрөг тэмдэгтэй үед модулаас хэрхэн гарахыг мэдэх тул системийг 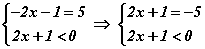 гэж хувиргавал тэгшитгэл 2-р тэнцэтгэл бишийг хангах нь тодорхой болно. Үнэхээр 2x+1=-5 нь тэгээс бага. Бодолтыг хийвэл
гэж хувиргавал тэгшитгэл 2-р тэнцэтгэл бишийг хангах нь тодорхой болно. Үнэхээр 2x+1=-5 нь тэгээс бага. Бодолтыг хийвэл 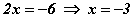 гэж гарна. Ингээд |2x+1|=5 тэгшитгэл x=2, x=3 гэсэн шийдүүдтэй гэж гарна.
гэж гарна. Ингээд |2x+1|=5 тэгшитгэл x=2, x=3 гэсэн шийдүүдтэй гэж гарна.
Сүүлийн тэгшитгэлийн бодолт |x|=3 тэгшитгэлийнхээс арай их болсон ч зарчмын хувьд юу ч өөр болоогүй. Тэгэхлээр тэгшитгэлийг бодох универсал алгоритм байж болохоор. Үүнийг дараагийн хичээлээс үзээрэй.





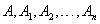 гэсэн төгсгөлөг цэгийн багц байна. Тэгвэл AB хэрчим дээр байгаа
гэсэн төгсгөлөг цэгийн багц байна. Тэгвэл AB хэрчим дээр байгаа 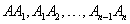 хэрчмүүд нь CD дээрх хэрчмүүдтэй тэнцүү бөгөөд A ба
хэрчмүүд нь CD дээрх хэрчмүүдтэй тэнцүү бөгөөд A ба 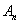 хооронд B цэг оршино.
хооронд B цэг оршино.
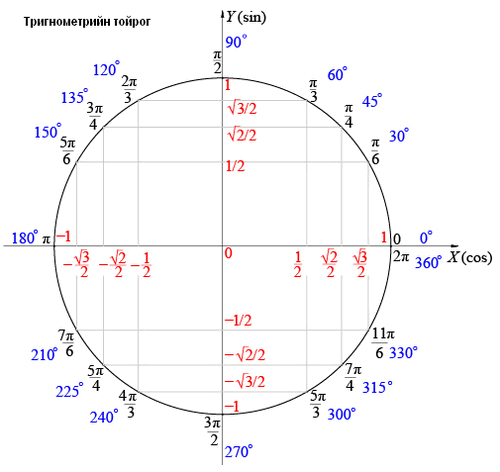
 тэгшитгэлийг бод.
тэгшитгэлийг бод.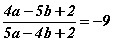 бол
бол 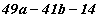 илэрхийллийн утгыг ол.
илэрхийллийн утгыг ол.