Прогресстой холбоотой бодлогууд элсэлтийн ерөнхий шалгалтанд ирэх нь бараг уламжлал. Бид энэ хичээлээр прогресстой хамааралтай бодлогуудын талаар авч үзэх болно. Үндсэн ойлголтыг Арифметик ба геометр прогресс хичээлээс аваарай. Прогрессын бодлогуудыг бодоход холбогдох томьёонуудыг мэдэж байхад тийм хүнд биш. Тригнометрийн тэгшитгэл, алгебрийн тэгшитгэл, илэрхийлэл хялбарчлах гэх мэтийн бодлогыг бодох тогтсон аргачлал, дүрэм байдаг бол прогресстой холбоотой бодлогыг бодох тодорхой аргачлалууд гэж байдаггүй бодлогын нөхцөлд тулгуурлан томьёогоо ашиглаад явдаг.
Энэ нь нэг талаас прогрессын бодлогуудыг амархан мэт харагдуулах боловч нөгөө талаас асуудал үүсгэдэг адармаатай. Ингээд прогресстой холбоотой бодлогуудын талаар авч үзье. Бодлогын бодолтыг үзэхээсээ өмнө санааг ашиглан өөрсдөө бодох гээд үзээрэй.
1. Бодлогын нөхцөлд прогресс гэдгийг шууд өгсөн байвал бодолт хөнгөн болно. Энд прогрессын ерөнхий гишүүний, нийлбэрийн, дараалсан 3 гишүүдийн хамаарлын томьёогоор асуудлыг шийдэх боломжтой. Жишээ авч үзье.
Бодлого 6.027 Элсэлтийн ерөнхий шалгалт 2014 A-23
a1=4, S5=40 байх арифметик прогрессийн d=q, a1=b1 нөхцөлийг хангах геометр прогрессийн 5-р гишүүнийг ол.
Санаа
Энэ бодлогын хувьд арифметик прогресс гэдгийг хэлсэн. Эхний гишүүн болон 5 гишүүний нийлбэр өгөгдсөн тул нийлбэрийн томьёогоор ялгавар /d/ олоод цааш геометр прогрессын 5-р гишүүнийг олоход хэцүү зүйл байхгүй.
Бодлого 6.029
Өсөх геометр прогресс үүсгэх гурван тооны 3 дахь нь 12 -той тэнцүү. Хэрвээ 12-ыг 9 -өөр соливол эдгээр гурван тоо нь арифметик прогресс үүсгэх бол тоонуудын нийлбэрийг ол.
Санаа
Энд бас л прогресс үүсгэх тоонууд гээд бодлогыг прогресстой холбоотойг шууд заан өгсөн байна. Эхний жишээний хувьд нийлбэр, эхний гишүүд гэсэн бол энэ жишээнд 3 тоо прогресс үүсгэх тухай байгаа тул танд шууд л дараалсан гурван гишүүний хамааралын томьёо орж ёстой.
Дээрх жишээнүүд шиг прогресс гэдгийг шууд заасан бодлогуудыг томьёогоо мэдэж байхад амархан шийдэх боломжтой. Гэтэл шалгалт шүүлэг дээр дандаа ийм бодлогууд ирээд байдаггүйг дараагийн хэсгээс харцгаая.
2. Прогрессын бодлого гэдэг нь мэдэгдэж байгаа ч математикийн өөр сэдэвтэй хавсарсан бодлогууд. Ийм бодлогууд сурагчдаас илүү хүчин чармайлт өөрөөр хэлбэл илүү мэдлэгийг шаардана. Жишээ нь
Бодлого 6.024 Элсэлтийн ерөнхий шалгалт 2007 A-15
Арифметик прогрессийн эхний гишүүн нь -27, ялгавар нь 5 бол эхний n гишүүний нийлбэрийн хамгийн бага утгыг ол.
Санаа
Эхний гишүүн, ялгавар өгөгдсөн тул нийлбэрийг илэрхийлэхэд амархан. Шууд томьёо байгаа. Харин нийлбэр n -ээс хамаарсан функц болно. Эндээс функцийн шинжилгээг ашиглах юм.
Бодлого 6.002
Дурын n гишүүний нийлбэр нь n ийн квадратыг 4-өөр үржүүлсэнтэй тэнцүү байдаг арифметик прогрессын эхний 6 гишүүний нийлбэрийг ол.
Санаа
Арифметик прогрессийн n гишүүний нийлбэрийн томьёоноос тэгшитгэл зохио.
Бодлогын өгүүлбэрт n гишүүний нийлбэр, хамгийн их бага утга олох гэх мэтээр дээрх жишээний нөхцлүүдтэй төстэй зүйл байвал өгөгдсөн n -ээс хамаарсан функцыг прогрессийн томьёонуудаар гаргаад цааш олох зүйлийг математикийн бусад аргуудыг ашиглан олох хэрэгтэй болно.
3. Бодлогын нөхцөлд прогресс гэдгийг заагүй бодлогууд. Ийм бодлогууд хамгийн адармаатай. Учир нь сурагчид эхлээд бодлогын нөхцөлд прогресс байгааг олж харах хэрэгтэй болдог. Бодлогууд тэгшитгэл, илэрхийлэл, өгууүлбэртэй бодлого гэх мэтээр маш олон төрлөөр байж болно. Ерөнхий хэлбэр нь голдуу дараалал байдлаар өгөгдсөн байдагийг тогтоох хэрэгтэй. Жишээ нь
Бодлого 6.022 Элсэлтийн ерөнхий шалгалт 2012 A-13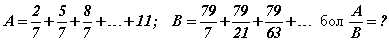
Санаа
A, B нь прогресс үүсгэж байгааг олж харах.
Бодлого 6.004
|x| < 0.5 бол 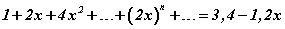 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Санаа
Дараалал прогресс үүсгэж байгааг батлах.
Бодлого 6.030
a=1,(4) бутархайг энгийн бутаргай болго.
Санаа
Бутархайг өөр хэлбэрээр бичээд прогресс байгааг олох
Эндээс прогрессийн бодлогууд энгийн мэт боловч нилээд асуудал үүсгэж болохоор нь харагдана. Бодлого бодох нэг үндэс бол нөхцлийг сайн ойлгох явдал. Энэ тухай ЭЕШ-г амжилттай өгөх арга нийтлэлээс үзээрэй. Нөхцлийг гүйцэд ойлгохгүйгээр бодолтыг эхэлбэл цаг хугацаа алдах цаашлаад буруу бодох нөхцөл бүрдэнэ. Иймээс бодлогын нөхцлийг ойлгон уг бодлогыг ямар арга хэрэгсэл ашиглан бодохоо тодорхойлсны дараа бодолтоо эхлэх хэрэгтэй.






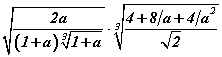 илэрхийллийг хялбарчил.
илэрхийллийг хялбарчил.