Вектор ба түүний үйлдлүүдийн талаар энэ хичээлээр авч үзье. Вектортой холбоотой бодлогууд дээр сурагчид будлих, алдаа гаргах нь элбэг байдаг. Ойлголт энгийн мэт боловч векторуудын нийлбэр, ялгавар, үржвэр зэргийг зөв ойлгохгүйгээр бодлого бодоход хүндрэл үүснэ. ЕБС-д энэ сэдвийн хичээлийг их өнгөцхөн үздэгээс сурагчид дутуу ойлгон улмаар бодлогод дээр дүрмүүдийг хэрэглэхдээ их сул байдаг. Иймээс вектор түүнтэй хийгдэх үйлдлүүдийг нэг мөр цэгцлэн тэдгээрийг бодлого бодоход ашиглаж сурахад хичээл зориулагдсан. Эхлээд ерөнхий ойлголтуудын талаар.
Материалыг бүртгэлтэй хэрэглэгч үзнэ.
how_to_regБүртгүүлэх




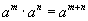
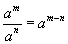
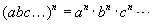
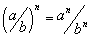
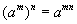
 тэгшитгэлийг бод.
тэгшитгэлийг бод.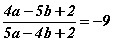 бол
бол 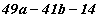 илэрхийллийн утгыг ол.
илэрхийллийн утгыг ол.