x2=a гэсэн дутуу квадрат тэгшитгэлийг авч үзье. Энд a - тодорхой тоо. Энэ тэгшитгэлийн шийд нь
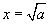болно.
Энд гурван тохиолдол гарна.
1. Хэрвээ a=0 бол x=0
2. Хэрвээ a нь эерэг тоо бол тэгшитгэл эерэг, сөрөг хоёр шийдтэй.
Жишээ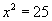
тэгшитгэл нь 5, -5 гэсэн хоёр шийдтэй. Шийдийг дараах хэлбэрээр 
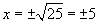гэж бичдэг.
Материалыг бүртгэлтэй хэрэглэгч үзнэ.
how_to_regБүртгүүлэхМэдээлэл таалагдсан бол найзуудтайгаа хуваалцаарай.
Нээгдсэн тоо: 1347 Төлбөртэй
Рационал бутархай гэдэг нь хуваар болон хүртвэр нь олон гишүүнтээс бүрдсэн бутархайг хэлнэ. Монгол хэлний орчуулга гэж байдаггүй байх. Гэхдээ олон гишүүнт хуваар болон хүртвэрт нь орсон бутархайг рационал гээд ойлгоход болно. Рационал бутархайтай ажиллах нь математикийн олон төрлийн бодлогыг бодох үндэс болдог учраас үүнийг сайтар эзэмшсэн байх ёстой. Бутархайг зөв эмхэтгэж сураагүй тохиолдолд энгийн илэрхийллийг ч бодож чадахгүйд хүрдэг. Үүнээсээ болоод сурагчид математикийг хүнд гэж бодон тооны хичээлээс айдаг бүр зугтаадаг болдог. Гэтэл математикийн шинжлэх ухаан нь бусдынхаа суурь тул үүнийг ойлгохгүйгээр өөр бусдад суралцан амжилтад хүрнэ гэдэг бараг мөрөөдөл. Энэ бол миний бодол. Одоо үндсэн асуудалдаа орцгооё.
Нээгдсэн тоо: 802 Бүртгүүлэх
Алгебр үзэж эхлэж байгаа сурагчдад тохиолддог эхний хүндрэл үсгүүд орж ирэх дараагийнх нь хаалт нээх байдаг. Хаалтыг алгебрийн илэрхийлэлүүдэд ихээр ашигладаг тул Алгебрийн илэрхийллүүд сэдвийн бодлогуудыг бодох явцад аяндаа цээжлэгдэх болно. Алгебрийн дүрэм, тоерем, томьёонуудыг шууд цээжлэх гэснээс илүү бодлогуудад ашиглан хэрэглэвэл илүү хурдан тогтоодог.
Хаалт нээх гэдэг бол хаалттай бичигдсэн илэрхийллийг түүнтэй тэнцүү хаалтгүй илэрхийллээр солихыг хэлнэ.
Нээгдсэн тоо: 15977 Нийтийн
Хичээлд хавтгайн геометрийн бодлого бодоход чухал хэрэгтэй гурвалжны биссектрисийн нэгэн чанарыг авч үзье. ABC гурвалжны B оройгоос түүний эсрэг орших AC тал дээрх D цэгт биссектрисийг буулгая.
Нээгдсэн тоо: 6204 Нийтийн
Тоо гэдэг ухагдхууныг хүмүүс маш эртнээс бий болгон ашиглан ирсэн. Эхлээд натурал тооны олонлог бий болон араас нь бутархай, эерэг иррационал тоонууд бий болсон. Орчин үеийн математикт тоонуудыг олон дэд олонлогт задлан үзэх болсон. Сурагчид эдгээр тоон олонлогуудын талаарх мэдлэг дутуугаас зарим нэгэн тэмдэглэгээг ч мэдэхгүй байх нь элбэг. Тоонуудын олонлогийн талаар сайн ойлгон тухайн олонлогт ямар тоонууд ордогийг мэдэж байх хэрэгтэй. Олонлогт багтах тоонуудыг сурагчид бараг бүгд мэддэг хирнээ ямар олонлог, хэрхэн тэмдэглэдэг, ямар шинжүүдтэй зэргийг мэддэггүй. Үүнээс болоод зарим бодлогын нөхцлийг буруу ойлгох, шийдийн олонлогийг буруу бичих зэрэг алдаануудыг гаргадаг. Иймээс тоон олонлогуудыг талаар мэдлэгтэй болцгооё.
функц өгөгдөв.
Нээгдсэн тоо : 2831
тэгшитгэлийн шийдийг ол.