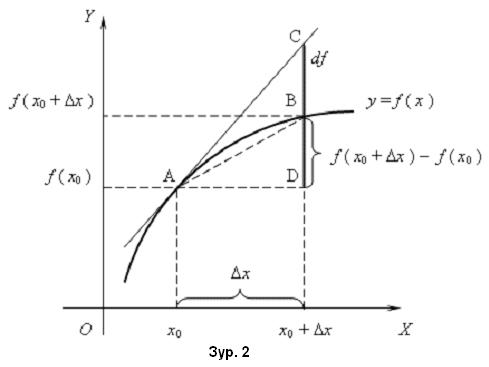
Дифференцал
Функцын уламжлал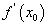 
, аргументын өөрчлөлт 
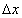ийн үржвэрийг функцын дифференциал гэнэ.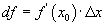 
/Зур. 2 / дээр дифференциалын геометр утгыг үзүүллээ. Энд df=CD
Уламжлал ба дифференцалын үндсэн шинжүүд
Хэрвээ x0 цэгт u(x) ба v(x) функцууд нь дифференциалчлагдах бол:
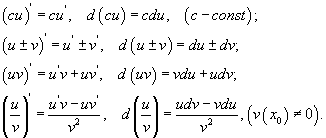
Төвөгтэй функцын уламжлал
h(x)=g(f(x)) аргумент нь функц байдаг төвөгтэй функцыг авч үзье. Хэрвээ x0 цэгт f функц нь уламжлалтай,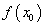 
цэгт g функц нь уламжлалтай бол x0 цэгт h функц нь уламжлалтай байх бөгөөд дараах томьёогоор тооцно.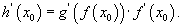 
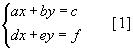Мэдээлэл таалагдсан бол найзуудтайгаа хуваалцаарай.
Нээгдсэн тоо: 803 Нийтийн
Арифметикийн үйлдлүүд нэг ба хоёрдугаар түвшингийн гэж хуваагдана.
Нээгдсэн тоо: 1332 Төлбөртэй
Тригнометрийн ямарч тэгшитгэлийг бодох үндсэн аргачлал бол анхдагч тэгшитгэлийг хувирган торигнометрийн энгийн тэгшитгэлүүдэд шилжүүлээд тэдгээрийн шийдийг олох байдаг. Иймээс тригнометрийн энгийн тэгшитгэлийн шийдийг цээжээр мэдэж байх хэрэгтэй. Энгийн тэгшитгэлийн шийдийг гаргаж буй аргачлалыг сайн ойлголгүй хүчээр цээжлсэнээс болоод тэгшитгэлүүдийн шийдүүдийг холих, тодорхой интервал дахь шийдийг тодорхойлох, орлуулгаас шийдийг олох гээд олон тохиолдолд асуудалд орох талтай.
Жич: Тригнометрийн энгийн тэгшитгэлийн шийдүүд хэрхэн гарч байгааг ойлгохгүйгээр шууд цээжилбэл та цаашид мартан тригнометр гэдэг ухагдхууныг мэддэггүй хүмүүсийн эгнээнд орно. Ихэнх хүмүүс энэ замаар явсан байдаг учраас математикийг хүнд хэцүү хичээл мэтээр ойлгон ярьдаг.
Хичээлээр cosx=a, sinx=a хэлбэрийн энгийн тэгшитгэлийн шийдийг хэрхэн тодорхойлохыг авч үзье.
Нээгдсэн тоо: 2093 Бүртгүүлэх
Арксинус, арккосинус, арктангенс, арккотангенс гэдэг ойлголтоос сурагчид нилээд айдаг. Эдгээр ухагдхууныг сайтар ойлгоогүйн улмаас түүнийг ашиглах, тэдгээртэй холбогдолтой бодлого бодохоос зайлсхийдэг. Өөрөөр хэлбэл айнаа л гэсэн үг. Гэхдээ эдгээр нь ойлгосон хүндээ тригнометрийн тэгшитгэлийг бодоход асар тус болдог энгийн л ойлголтууд гэдгийг та энэ хичээлийн эцэст мэдэн авах болно.
Синус, косинус, тангенс, котангенс талаар мэдэж байхад илүүдэхгүй. Тэдгээрийн зарим өнцгүүдийн утгууд гээд хамгийн ерөнхий зүйлийг мэдэж байхад асуудал үүсэхгүй ойлгоно.
Нээгдсэн тоо: 7345 Төлбөртэй
Олон өнцөгт хавтгайн хэсгүүдээс бүрдсэн биетийг олон талт гэнэ. Эдгээр олон өнцөгтийг талууд, тэдгээрийн талуудыг ирмэгүүд, оройнуудыг нь олон талтын оройнууд гэнэ. Хоёр оройг холбосон нэг тал дээр оршдоггүй хэрчмийг олон талтын диагнал гэдэг. Бүх диагнал нь олон талт дотроо байдаг биетийг гүдгэр олон талт гэнэ.
Призм
Призм гэдэг нь /Зур. 79/ хоёр тал нь ( призмийн суурь) ABCDEF ба abcdef гэсэн паралел ижил олон өнцөгт , бусад талууд нь 
шулуунуудтай паралел 
паралелграм хавтгайнуудаас бүрдсэн олон талт юм. 
паралелграмуудыг хажуу талууд, 
шулуунуудыг хажуу ирмэгүүд гэдэг. Нэг сууриас нөгөө суурьт буулгасан дурын перпендикуляр нь призмийн өндөр болно.
илэрхийллийн хялбарчил.