Өнцөг
Огтлолцсон хоёр шулууны хоорондох өнцгийг хавтгайн геометрийн адилаар хэмжинэ. Учир нь эдгээр шулууныг дайруулан хавтгай татаж болдог. Паралел хоёр шулууны хоорондын өнцөг нь 0 эсвэл 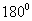 . Зөрсөн AB ба CD /Зур. 70/ хоёр шулууны хоорондын өнцгийг дараах байдлаар тодорхойлно.
. Зөрсөн AB ба CD /Зур. 70/ хоёр шулууны хоорондын өнцгийг дараах байдлаар тодорхойлно.
Дурын O цэгийг дайруулаад OM || AB ба ON || CD байх OM, ON цацрагийг татна. Тэгвэл AB ба CD гийн хоорондох өнцөг нь NOM тэй тэнцүү гэж үзнэ. Өөр хэлбэл AB ба CD шулууныг өөртөө нь паралел байдлаар огтлолцох хүртэл нь шилжүүлнэ гэсэн үг. Тухайлбал O цэгийг AB ба CD шулуунуудын аль нэг дээр авч болно. Энэ тохиолдолд O цэг нь хөдөлгөөнгүй байна.
Материалыг тусгай эрхтэй хэрэглэгч үзнэ.
request_quoteТусгай эрх авах




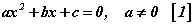 хэлбэрийн тэгшитгэлийг
хэлбэрийн тэгшитгэлийг 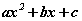 илэрхийллийг
илэрхийллийг  илэрхийллийг хялбарчил.
илэрхийллийг хялбарчил.
 задаргааны 6-р гишүүнийг ол.
задаргааны 6-р гишүүнийг ол.