Геометрийн тойрог, дугуй дүрсүүдийн ялгааг сайн ойлгодоггүй байх тохиолдол элбэг. Зарим сурагчид эдгээрийн ялгааг ойлгоогүйн улмаас бодлогын нөхцлийг ойлгохгүй бодох аргаа ч олохгүй байх тохиолддол гардаг. Тойрог, дугуйн ялгааг ойлгохын тулд эхлээд Тойрог хичээлийг үзэхийг зөвлөе.
Дугуй гэдэг нь тойргоор хязгаарлагдсан хавтгайн хэсэг юм.
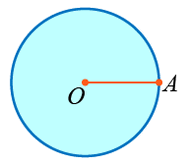
Дугуйг хязгаарлаж байгаа тойргийн төв дугуйн төв харин дугуйн төвөөс тойргийн дурын цэг хүртлэх зайг дугуйн радиус гэж нэрлэдэг. Иймээс зурагт үзүүлсэн дугуйн төв O харин OA бол түүний радиус. Эндээс ойлголтын зөрүү үүсдэг. Тойрог хичээлд дээрх зурагт үзүүлсэн дугуйг хязгаарлаж байгаа хөх битүү шугамыг л тойрог гэж тодорхойлсон байгаа. Харин энэ битүү шугамаар хязгаарлагдаж буй хавтгайн цэнхэр хэсгийг дугуй гээд байгаа хэрэг. Тойрог, дугуй хоёрт төв, радиусууд ижилхэн боловч тооцоологдох шинжүүд нь өөр.
Дугуйн талбай, тойргийн урт.
Дугуй хавтгайн хэсэг учраас түүнд талбай гэсэн ойлголт бий. Дугуйн талбай π тоог дугуйн радиусийн квадратаар 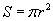 үржүүлсэнтэй тэнцүү. Дугуйн диаметр түүний радиусийг хоёроор үржүүлсэнтэй тэнцүү тул радис /r/ диаметр /D/ -г хоёрт хуваасантай тэнцүү. Эндээс дугуйн талбайг диаметрээр олох томьёо
үржүүлсэнтэй тэнцүү. Дугуйн диаметр түүний радиусийг хоёроор үржүүлсэнтэй тэнцүү тул радис /r/ диаметр /D/ -г хоёрт хуваасантай тэнцүү. Эндээс дугуйн талбайг диаметрээр олох томьёо 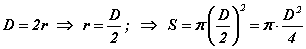 гэж гарна.
гэж гарна.
Тойрог шугамаар тодорхойлогддог учраас түүнд талбай гэж байдаггүй харин урт гэсэн ойлголт бий. Тойргийн урт π тоо тойргийн радиусийн үржвэрийг хоёроор үржүүлсэн 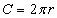 тэнцдэг.
тэнцдэг.
Санамж: Хавтгайн геометрийг үзэж эхлэж байгаа сурагчид тойрог, дугуйн ялгааг ойлгоогүйгээс эдгээр ойлголтыг холин бодлогын нөхцлийг буруу ойлгох тохиолдол ихээр гаргадаг.
Дугуйн сектор, Секторийн талбай.
Дугуйн хоёр радиусаар хязгаарлагдсан дугуйн хэсгийг сектор гэнэ.
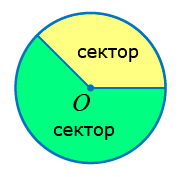
Иймээс хоёр радиус дугуйг хоёр секторт хуваана. Зургийг хар. Дугуйн секторийн талбайг хэрхэн олохыг
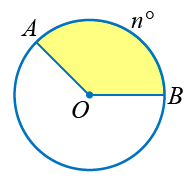
дээрх зурагт үзүүлсэн сектороор авч үзье. Дугуйн төв O болон AO, OB радиусуудаар үүссэн сектор n0 градусийн хэмжээтэй AOB нумаар хязгаарлагдсан гэж үзье. Тэгвэл ерөнхий төгсгөлтэй хоёр нумын градусийн хэмжээсийн нийлбэр 360 гэдгийг Төв өнцөг, түүний шинжүүд хичээлээс мэдэх учраас O болон AO, OB радиусуудаар үүссэн секторийн талбай нь дугуйн талбайг 360 -д хуваагаад AOB нумын хэмжээс n -ээр үржүүлсэнтэй тэнцүү байна. Математик бичлэгээр 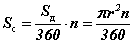 байна. Секторийн талбайн илэрхийллийг
байна. Секторийн талбайн илэрхийллийг 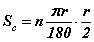 гэж задлан бичиж болно. Энд
гэж задлан бичиж болно. Энд 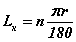 нь секторийн нумын урт. Эндээс секторийн талбай
нь секторийн нумын урт. Эндээс секторийн талбай 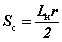 буюу тухайн секторийн нумын уртыг дугуйн радиусийн хагасаар үржүүлсэнтэй тэнцүү гэж гарна.
буюу тухайн секторийн нумын уртыг дугуйн радиусийн хагасаар үржүүлсэнтэй тэнцүү гэж гарна.
Сегмент. Сегментийн талбай.
Сегмент гэдэг нь нум болон түүнд тулсан хөвчөөр хязгаарлагдсан дугуйн хэсэг юм.
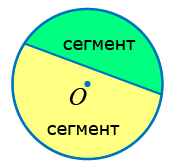
Иймээс дурын хөвч дугуйг хоёр сегментэд хуваана. Зургийг хар. Хөвч, нум ойлголтыг мартсан бол Тойрог хичээлийг үзээрэй.
Сегментийн талбай
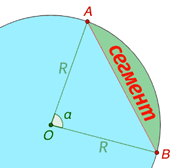
Зурагт дугуйн сегментийг ногоон өнгөөр будсан. Энд AB хэрчим бол хөвч, A ба B цэгүүдийн хоорондох тойргийн хэсэг бол тойргийн нум, R - дугуйн радиус, α - секторийн өнцөг гэдгийг сануулъя.
Радиус болон градусаар өгөгдсөн төв өнцөгөөр буюу α - өнцөг градусаар өгөгдсөн үед 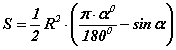 томьёогоор сегментийн талбайг олдог.
томьёогоор сегментийн талбайг олдог.
Санамж: Тооцоонд π -гийн утгыг ойролцоогоор 3,14 гэж тооцдог.
Радиус болон радианаар өгөдсөн секторийн өнцгөөр буюу буюу α - өнцөг радианаар өгөгдсөн үед 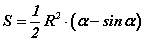 томьёогоор сегментийн талбайг олдог.
томьёогоор сегментийн талбайг олдог.





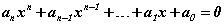 хэлбэрээр өгөгдсөн тэгшитгэлийг ойлгоно. Энд an, an-1, ... , a0 - өгөгдсөн тоонууд, x - үл мэдэгдэгч, n - үл мэдэгдэгчийн хамгийн их зэрэг буюу алгебрийн тэгшитгэлийн зэрэг гэж нэрлэнэ. Алгебрийн тэгшитгэлүүдийн төрлүүд болон тэдгээрийг бодох аргуудтай танилцгаая.
хэлбэрээр өгөгдсөн тэгшитгэлийг ойлгоно. Энд an, an-1, ... , a0 - өгөгдсөн тоонууд, x - үл мэдэгдэгч, n - үл мэдэгдэгчийн хамгийн их зэрэг буюу алгебрийн тэгшитгэлийн зэрэг гэж нэрлэнэ. Алгебрийн тэгшитгэлүүдийн төрлүүд болон тэдгээрийг бодох аргуудтай танилцгаая. функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол. тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.