Ялгавар дахь хасагдагчийг эсрэг тэмдэгтэйгээр авбал ялгаварыг нийлбэрээр сольж болно. Нийлбэрийн энэ шинжийг
a - b = a + (-b)
ерөнхий томьёогоор илэрхийлж болно. Эндээс дурын ялгаварыг нийлбэрээр сольж болохыг энэ томьёо илэрхийлнэ. Иймээс алгебрт хасах, нэмэх үйлдэлүүд оролцсон дурын илэрхийллийг нийлбэр гэж үзэж болно.
Жишээ нь 2x - y2 = 2x + (-y2); -21 + n - m = - 21 + n + (-m) гэх мэтээр. Ийм илэрхийллүүдийг алгебрийн нийлбэр гэдэг.
Алгебрийн нийлбэр гэдэг нь эерэг ба сөрөг тоонуудын нийлбэр хэлбэрээр илэрхийлж болох илэрхийлэл юм.
Санамж: Алгебрийн нийлбэрт эерэг тооны өмнө + тэмдэгийг тавихгүйгээр илэрхийллийн эхэнд байгаа сөрөг тоо хаалтанд авахгүйгээр хураангуйлж бичдэг. Жишээ нь (-5) + (+7) = -5 + 7. Үүнээс гадна алгебрийн илэрхийлэлд + тэмдэгтэй нэмэгдхүүн байвал түүнийг илэрхийллийн эхэнд бичдэг. Жишээ нь -2x - y + 3z илэрхийллийг 3z - 2x - y гэж бичнэ.
Алгебрийн нийлбэрийн шинжүүд
Дурын нийлбэрт нэмэгдхүүнүүдийг ямарч байдлаар байрыг солих, бүлэглэн нэгтгэж болно. Өөрөөр хэлбэл нийлбэрийн байр солих, бүлэглэн нэгтгэх шинжүүдийг ашиглах боломжтой.
a + b = b + a
a + b + c = (a + b) + c = a + (b + c) = (a + c) + b
Жишээ нь
10 + (-7) = -7 + 10 = 3
-7 + 28 + (-13) + 12 = (-7 + (-13)) + (28 + 12) = -20 + 40 = 20
Зөвлөмж: Сүүлийн жилүүдэд ЭЕШ -ийн сонгох хэсгийн материалд онолын ерөнхий мэдлэгийг сорьсон бодлого гэхээсээ асуулт хэлбэрийн даалгаварууд орж ирэх болсон. Иймээс онолын ерөнхий мэдлэгийн бэлтгэлийг сайн хийхийг зөвлөе. Жишээ нь ямар нэгэн илэрхийлэл өгөгдөөд түүний алгебрийн нийлбэрийг олох даалгавар байвал танд бодоод байх зүйл байхгүй зөвхөн онолоор яаж бичдэгийг л мэдэх хэрэг гарна. Иймээс ухагдхууныг сайн ойлгон аваад өөрөө хэсэг илэрхийллийг алгебрийн нийлбэрээр илэрхийлэн дасгал хийгээрэй.





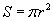 томьёогоор илэрхийлэгдэнэ; Хоёр хувьсагчийн функционал хамаарал хэсэгт авч үзсэн дээш шидэгдсэн биеийн хүрэх өндөр h, нийт хугацаа T хоёрын хамаарал гэх мэт. Агаарын эсэргүүцэл, дэлхийн таталтын хүч өндрөөс хамаардаг зэргийг тооцоогүй учраас энэ нь ойролцоо томьёо юм. Функционал хамааралыг томьёогоор илэрхийлэх боломжгүй эсвэл томьёо нь тооцоо хийхэд тохиромж муутай байх тохиолдол бас байдаг. Ийм үед функцыг хүснэгт эсвэл графикаар үзүүлдэг.
томьёогоор илэрхийлэгдэнэ; Хоёр хувьсагчийн функционал хамаарал хэсэгт авч үзсэн дээш шидэгдсэн биеийн хүрэх өндөр h, нийт хугацаа T хоёрын хамаарал гэх мэт. Агаарын эсэргүүцэл, дэлхийн таталтын хүч өндрөөс хамаардаг зэргийг тооцоогүй учраас энэ нь ойролцоо томьёо юм. Функционал хамааралыг томьёогоор илэрхийлэх боломжгүй эсвэл томьёо нь тооцоо хийхэд тохиромж муутай байх тохиолдол бас байдаг. Ийм үед функцыг хүснэгт эсвэл графикаар үзүүлдэг. функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол. тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.