Ямар нэгэн зүйл /обьект/ эсхүл хийгдэж буй үйлдлийн тоог мэдэхийн тулд тэдгээрийг тоолох хэрэгтэй. Тоолол гэдэг нь ямар нэгэн тоон үзүүлэлтийг тооцох үйлдэл эсхүл тооллогоор илэрхийлэгдэнэ. Тоололд орж буй тусдаа обьект бүр эсхүл тусдаа үйлдэл бүрийг нэгж гэнэ. Нэгж гэдэг нь тусдаа обьектын хийсвэрлэлийг илэрхийлэх тоо юм. Тоололын үр дүн буюу тоологдсон нэгжийн нийлбэрийг тоо гэж нэрлэнэ.
Тоо гэдэг нь тооллого эсхүл ямар нэгэн өөр тооцоололын үр дүн. Тоог харьцуулалт, обьектийн дугаарлалт, тэдгээрийн хэсгийн тоон шинж чанарыг тодорхойлоход ашиглана. Математикийн ухагдхуунуудыг үгээр тайлбарлах төвөгтэй мэт боловч үүнийг сурах хэрэгтэй. Ухагдхууныг дараах жишээнээс илүү ойлгон аваарай.
Хайрцагт байгаа харандаануудын тоололд харандаа бүрийг нэгж гэж үзээд нэгжийн тоололын үр дүнд бид тоо авна.
Тоо "хэд вэ?" асуултад хариу өгөх боломжийг өгнө. Жишээ нь "хайрцагт хэдэн харандаа байна вэ" гэх мэтээр
Тоог үгээр болон тусгай тэмдэгтүүд ашиглан бичгээр илэрхийлэх хоёр арга бий. Тоог үгээр илэрхийлэхийг амаар буюу үгээр дугаарлах харин бичгийн тэмдэгтээр илэрхийлэхийг бичгэн дугаарлалт гэнэ.
Нэрлэсэн болон тодорхойгүй тоонууд
Тооллогын үр дүнгээр гарсан нэгжийн тоонд тоолж буй зүйлийн нэр цуг байгаа тоог нэрлэсэн тоо гэнэ. Жишээ нь таван алим, найман гадил гэх мэтээр. Эдгээрийг нэрлэсэн тоо гэнэ.
Тооллогын нэгжийн нэрийг агуулаагүй тоог тодорхойгүй тоо гэнэ. Жишээ нь тав, долоо, ес гэх мэтээр. Тоонууд ямар нэгэн зүйлийн нэрийг агуулаагүй тул тодорхойгүй тоонууд.
Олонлог
Математикт дурын бүлэг обьектуудыг олонлог гэж нэрлэж болно. Бүлгийн обьектийг олонлогийн элемент гэнэ.
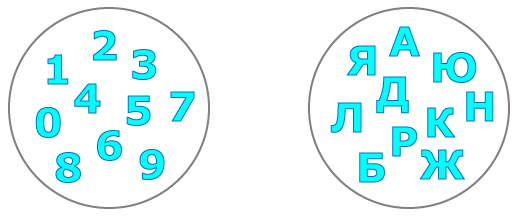
Дээрх зурагт цифрүүд болон үсгүүдийн хоёр олонлогийг дүрсэлсэн байгаа. Эндээс олонлог гэдгийг ямар нэгэн ерөнхий шинжээр нэгдсэн обьектуудын бүлэг гэж ойлгож болно.
Олонлогууд нэг ижил обьектуудаас бүрдэж байвал тэдгээрийг тэнцүү харин өөр өөр обьектуудаас бүрдсэн бол тэнцүү биш гэнэ.
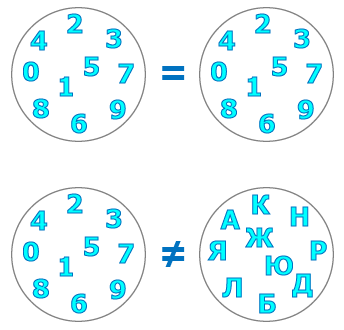
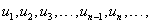тэмдэглэгээ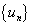 
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.