Арифметикийн үйлдлүүдийн шинжүүдийг мэдэхгүй ч хүмүүс тэдгээрийг тооцоонд өргөн ашигладаг. Энэ удаа үржвэрийн шинжүүдийг аьч үзье.
Байр солих шинж.
Үржигдхүүнүүдийн байрыг солиход үржвэр өөрчлөлгдөхгүй. Өөрөөр хэлбэл үржвэрт орж буй гишүүдийн байрыг солиход үржвэрт нөлөөлөхгүй гэсэн үг. Эндээс дурын a, b тоонууд эсхүл илэрхийллийн хувьд a·b=b·a байна.
Жишээ
6·7=7·6 = 42
4·2·3=3·2·4 = 24
a·b·c=c·a·b=b·c·a
Бүлэглэн үржүүлэх
Гурав болон түүнээс дээш үржигдхүүнтэй үржвэрийн дурын бүлэг үржигдхүүнүүдийг тэдгээрийн үржвэрээр солиход үржвэр өөрчлөгдөхгүй. Иймээс дурын a, b, c тоонууд эсхүл илэрхийллийн хувьд a·b·c=(a·b)·c=a·(b·c) тэнцэл үнэн.
Жишээ
3·2·5=3·(2·5)=3·10=30
3·2·5=(3·2)·5=6·5=30
Бүлэглэн үржих шинжийг олон тоонуудыг үржвэрийг хөнгөн хийхэд ашигладаг.
Жишээ нь 25·15·4 үржвэрийг тооцохдоо үржигдхүүнүүдийг үржвэрт орсон дарааллаар (25·15)·4=375·4=1500 гэж үржүүлснээс бүлэглэх шинжийг ашиглан 25·15·4=(25·4)·15=100·15=1500 гэж тооцох нь хамаагүй хялбар. Өөрөөр хэлбэл эхлээд 25·4=100 гэдгийг тооцоод дараа нь 15 -аар үржүүлнэ.
Олон тоонуудын үржвэрийг олохдоо тэдгээрийг дурын байдлаар сэлгэх /байрыг солих/, бүлэглэн нэгтгэж үржиж болно гэдгийг тогтоон аваарай.
Хэсэгчлэн үржүүлэх
Хэсэгчлэн үржүүлэх шинж нийлбэр ба ялгаварын гэсэн хоёр төрөлтэй.
- Нийлбэрийг тоогоор үржүүлэхдээ нэмэгдхүүн бүрийг тухайн тоогоор үржүүлээд гарсан үржвэрүүдийг нэмнэ. Өөрөөр хэлбэл a, b, c тоонууд эсхүл илэрхийллийн хувьд a·(b+c)=a·b+a·c тэнцэл үнэн.
Жишээ
(a+b+с+d)·k=a·k+b·k+c·k+d·k
(5+2+3+10)·5=5·5+2·5+3·5+10·5
- Ялгаварыг тоогоор үржүүлэхдээ хасагдагч ба хасагч бүрийг тухайн тоогоор үржүүлээд хасагдагч болон тухайн тооны үржвэрээс хасагч бүрийг тухайн тоогоор үржүүлсэн үржвэрүүдийг хасна. Өөрөөр хэлбэл a, b, c тоонууд эсхүл илэрхийллийн хувьд a·(b-c)=a·b-a·c тэнцэл үнэн.
Жишээ
(a-b-с)·d=a·d-b·d-c·d
(15-3-2)·5=15·5-3·5-2·5
Хэсэгчлэн үржүүлэх шинжээр үржвэрийг нийлбэр, ялгаварт шилжүүлэхийг хаалт нээх ч гэж ярьдаг. Жишээ нь m·(a+b)=m·a+m·b; m·(a-b)=m·a-m·b
Эсрэгээрээ нийлбэр, ялгаварыг үржвэрт шилжүүлэхийг ерөнхий үржвэрийг хаалтын өмнө гаргах гэж ярьдаг. Жишээ нь m·a+m·b=m·(a+b); m·a-m·b=m·(a-b)
Тэгээр үржих шинж
Ямарч тоог тэгээр үржихэд үржвэр тэг байна. Өөрөөр хэлбэл үржвэр дэх аль нэгэн үржигдхүүн тэг бол үржвэр тэг байна.
Жишээ
a·0=0
0·a·b·c=0
Зөвлөмж:
- Алгебр сэдвийг эхлэн үзэж байгаа сурагчдад зориулагдсан тул хичээлүүдийг аль болохоор богино зөвхөн нэг сэдвийн хүрээнд боловсруулсан.
- Хичээлийг үзээд жишээний дагуу өөрсдөө илэрхийлэл зохиогоод шинжүүдийг хэрэглэн үзвэл илүү хурдан тогтоох болно.
- Нэмэгдхүүн, хасагдагч гэх мэт илэрхийлэлийн гишүүдийн нэрийг маш сайн тогтоон аваарай.
- Эцэг эхчүүд бага насны хүүхэддээ туслан хамт үзвэл илүү өгөөжтэй.





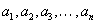 гэсэн n ширхэг ялгаатай элементийг авъя. Зөвхөн байрыг нь солих замаар бүх боломжит хувилбарыг гаргая. Ингэхдээ хувилбар болгонд n ширхэг элемент байна. Ийм байдлаар гаргаж авсан хувилбар бүрийг
гэсэн n ширхэг ялгаатай элементийг авъя. Зөвхөн байрыг нь солих замаар бүх боломжит хувилбарыг гаргая. Ингэхдээ хувилбар болгонд n ширхэг элемент байна. Ийм байдлаар гаргаж авсан хувилбар бүрийг 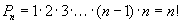
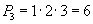 болно. Үнэхээр дээрх 3 элементээс abc, acb, bac, bca, cab, cba гэсэн 6 сэлгэмэл гаргаж болно.
болно. Үнэхээр дээрх 3 элементээс abc, acb, bac, bca, cab, cba гэсэн 6 сэлгэмэл гаргаж болно.
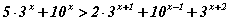 тэнцэтгэл бишийг бод.
тэнцэтгэл бишийг бод.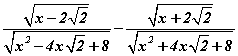 илэрхийллийн x=3 утгыг ол.
илэрхийллийн x=3 утгыг ол.