Алгебрийн тэгшитгэл гэдэгт 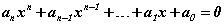 хэлбэрээр өгөгдсөн тэгшитгэлийг ойлгоно. Энд an, an-1, ... , a0 - өгөгдсөн тоонууд, x - үл мэдэгдэгч, n - үл мэдэгдэгчийн хамгийн их зэрэг буюу алгебрийн тэгшитгэлийн зэрэг гэж нэрлэнэ. Алгебрийн тэгшитгэлүүдийн төрлүүд болон тэдгээрийг бодох аргуудтай танилцгаая.
хэлбэрээр өгөгдсөн тэгшитгэлийг ойлгоно. Энд an, an-1, ... , a0 - өгөгдсөн тоонууд, x - үл мэдэгдэгч, n - үл мэдэгдэгчийн хамгийн их зэрэг буюу алгебрийн тэгшитгэлийн зэрэг гэж нэрлэнэ. Алгебрийн тэгшитгэлүүдийн төрлүүд болон тэдгээрийг бодох аргуудтай танилцгаая.
1. Шугаман тэгшитгэл
n=1 байхад дээрх бичлэг ax+b=0 хэлбэртэй болох бөгөөд ийм төрлийн тэгшитгэлийг шугаман тэгшитгэл гэх бөгөөд дараах аргаар бодно.
- Хэрвээ a≠0, b бодит тоо байвал x=b/a шийдтэй, Жишээ. x-3=2-4x ⇒ x+4x=2+3 ⇒ 5x=5 ⇒ x=1
- Хэрвээ a=0, b=0 бол x дурын тоо байна. Жишээ. 2x+3=5x+5-3x-2 ⇒ 2x-5x+3x=5-2-3 ⇒ 0=0 ⇒ x -дурын тоо
- Хэрвээ a=0, b≠0 бол тэгшитгэл шийдгүй. Жишээ. 2x+1=5x+5-3x-2 ⇒ 2x-5x+3x=5-2-1 ⇒ 0=2 ⇒ шийдгүй.
2. Квадрат тэгшитгэл
n=2 байхад дээрх бичлэг ax2+bx+c=0 хэлбэртэй болох бөгөөд ийм төрлийн тэгшитгэлийг квадрат тэгшитгэл гэх бөгөөд 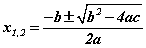 томьёогоор эсвэл Виетийн
томьёогоор эсвэл Виетийн 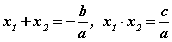 теоремоор бодогдоно. Дэлгэрэнгүй мэдээллийг Квадрат тэгшитгэлийг бодох хичээлээс үзээрэй.
теоремоор бодогдоно. Дэлгэрэнгүй мэдээллийг Квадрат тэгшитгэлийг бодох хичээлээс үзээрэй.
3. Рационал бутархай төрлийн тэгшитгэл.
Ийм тэгшитгэлийг доорх схемээр бодно.
- Тэгшитгэлийн бүх гишүүдийг тэнцүүгийн тэмдгийн зүүн талд гаргана.
- Тэгшитгэлийн зүүн талын бүх гишүүдийг ерөнхий хуваарьт оруулна. Өөрөөр хэлбэл тэгшитгэлийг
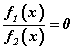 хэлбэрт оруулна.
хэлбэрт оруулна. - f2(x)≠0 үед f1(x)=0 тэгшитгэлийг бодно.
Бодлого 3.046 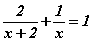 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Рационал бутархай хэлбэрийн тэгшитгэлийг бодохдоо хуваарийг тэгтэй тэнцүүлэх үл мэдэгдэгчийн утгыг заавал тооцож тэдгээрийг тэгшитгэлийн шийдээс хасах хэрэгтэйг санаарай.
4. Бүлэглэх арга.
Тэгшитгэлийн гишүүдийг бүлэглэн илэрхийллийг эмхэтгэх аргуудыг ашиглан боломжтой бол тэгшитгэлийн зүүн хэсгийг үржигдхүүнүүдийн үржвэр хэлбэрт оруулаад баруун хэсэгт тэг үлдээнэ. Дараа нь үржигдхүүн бүрийг тэгтэй тэнцүүлэн бодож шийдийг олох арга.
Бодлого 3.047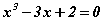 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Алгебрийн тэгшитгэлийг бодоход илэрхийллийг үржигдхүүнд задлах аргуудыг ихээр ашигладагийг дээрх жишээ баталж байна.
5. Орлуулах арга
Тэгшитгэлд давтагдаж байгаа илэрхийллийг шинэ үл мэдэгдэгчээр орлуулаад тэгшитгэлийг энгийн хэлбэрт шилжүүлэн бодоод гарсан шийдийг орлуулгад буцаан тавих замаар анхдагч тэгшитгэлийн шийдийг олох универсал арга. Аргыг алгебрийн гэлтгүй өөр бусад төрлийн тэгшитгэлүүдийг бодоход өргөнөөр ашигладаг.
Бодлого 3.048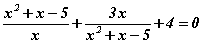 тэгшитгэлийн шийдүүд
тэгшитгэлийн шийдүүд 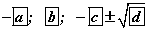 бол a, b, c, d -г ол.
бол a, b, c, d -г ол.
Арай хүндхэн тохиолдолд тэгшитгэлд эхмэтгэл хийсний дараа орлуулга харагдаж болно. Жишээ нь
Бодлого 3.049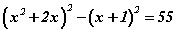 тэгшитгэлийг бод.
тэгшитгэлийг бод.
6. Сонгох арга.
Дээд эрэмбийн 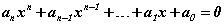 тэгшитгэлүүдийг бодохдоо p/q хэлбэрийн шийдийг хайх хэрэгтэй. Энд p - a0 -ийн хуваагч, q - an -ийн хуваагч байх анхны тоонууд байна. Арга нь илэрхийллийг үржигдхүүнд задлах олон гишүүнтийг хоёр гишүүнтэд хуваах аргатай нягт холбоотой байдаг тул холбогдох хичээлийг үзнэ үү.
тэгшитгэлүүдийг бодохдоо p/q хэлбэрийн шийдийг хайх хэрэгтэй. Энд p - a0 -ийн хуваагч, q - an -ийн хуваагч байх анхны тоонууд байна. Арга нь илэрхийллийг үржигдхүүнд задлах олон гишүүнтийг хоёр гишүүнтэд хуваах аргатай нягт холбоотой байдаг тул холбогдох хичээлийг үзнэ үү.
Бодлого 3.050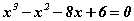 тэгшитгэлийг бод.
тэгшитгэлийг бод.
7. Модул агуулсан тэгшитгэлийг бодох.
Модул агуулсан тэгшитгэлийг бодохдоо модулийн тодорхойлолт болон интервалын аргыг ашиглана. Аргын ерөнхий схем нь
- Тэгшитгэлийн модулд байгаа илэрхийллүүдийг тэгтэй тэнцүүлэн утгыг олно.
- Олдсон утгуудыг тоон тэнхлэгт тэмдэглэнэ.
- Тоон тэнхлэгийн хуваагдсан интервал бүрд тэгшитгэлийн шийдийг тооцно.
Бодлого 3.051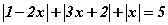 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Зарим тохиолдолд модулийн чанарыг ашиглан модулаас салж болно.
Бодлого 3.052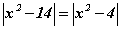 тэгшитгэлийг бод.
тэгшитгэлийг бод.





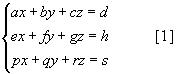 хэлбэрийн тэгшитгэлийн системийг
хэлбэрийн тэгшитгэлийн системийг 
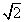
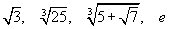
 илэрхийллийг хялбарчил.
илэрхийллийг хялбарчил.
 задаргааны 6-р гишүүнийг ол.
задаргааны 6-р гишүүнийг ол.