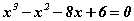тэгшитгэлийг бод.
Бодолт
Энд an=1, a0=6. Өөрөөр хэлбэл хамгийн их зэрэгтэй гишүүний коэффиициент 1, сул гишүүн 6 гэсэн үг. Иймээс тэгшитгэлийн шийдийг 6 -гийн хуваагчид болох ±1, ±2, ±3 дотроос хайх хэрэгтэй. Шалгалтаар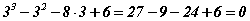 
гэдгээс тэгшитгэлийн нэг шийд 3 болох нь батлагдана. Одоо олон гишүүнтийг x-3 хоёр гишүүнтэд хуваавал x2+2x-2 ногдвор гарна. Эндээс өгөгдсөн тэгшитгэлийг 
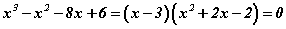гэж бичиж болох бөгөөд шийдийг олбол 
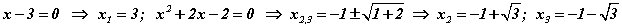гарна.
Олон гишүүнтийг хоёр гишүүнтэд хуваах аргын талаар Бодлого бодож сурах нь V хичээлээс үзээрэй.
Хариу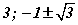
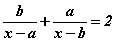тэгшитгэлийг бод.
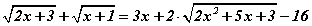тэгшитгэлийг бодъё. Тэгшитгэлийн тодорхойлогдох муж нь 
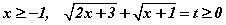гэж орлуулбал анхны тэгшитгэл 
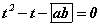тэгшитгэлд шилжинэ. Эндээс 
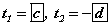гэж гарах ба t2<0 тул нөхцөлд тохирохгүй. Орлуулгаа буцаан бодвол тэгшитгэлийн шийд 
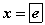гэж гарна.
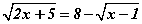тэгшитгэлийг бод.
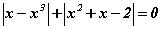тэгшитгэлийг бод.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.