Хэрвээ X хэсэгт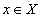 
байх x болгоны хувьд 
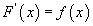бол тасралтгүй F(x) функцыг f(x) ийн эх функц гэнэ.
Жишээ
(-∞,+∞) мужид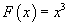 
функц нь 
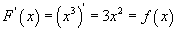учраас 
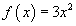ын эх функц болно. Мөн түүнчлэн x3+13 ийн уламжлал нь 3x2 тул x3+13 нь 
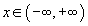болгоны хувьд 3x2 ийн эх функц нь болно. 13 оронд дурын тогтмол авч болох нь ойлгомжтой.
Иймээс эх функцыг олох бодлого нь хязгааргүй олон шийдтэй. Энэ байдал нь тодорхойгүй интегралын тодорхойлолтод тусгалаа олсон байдаг.
X хэсэгт f(x) функц нь түүний эх функцуудын олонлог юм.
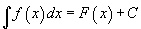гэж бичдэг. Энд C - интегралчлалын тогтмол гэж нэрлэдэг дурын тогтмол болно.
Тодорхойгүй интегралын үндсэн шинжүүд
- Тогтмолыг интералын тэмдгийн гадна гаргаж болно.
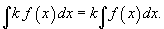
- Нийлбэрийн интеграл нь нэмэгдхүүн тус бүрийн интегралын нийлбэртэй тэнцүү.
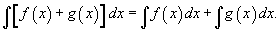
- Интегралын уламжлал нь интеграл доторх функцтай тэнцүү.
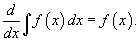
- Функцын дифференциалын интеграл нь энэ функц дээр интегралчлалын тогтмолыг нэмсэнтэй тэнцүү.
нь x0 цэгт дифференциалчлагдаж байвал түүнийг f(x) функцын x0 цэг дээрх хоёрдугаар эрэмбийн уламжлал / 
гэж тэмдэглэнэ./ гэнэ.
цэгт y=f(x) функцын графикийн муруйд татсан шүргэгчийн доор байрлаж байвал f(x) функцыг (a,b) интервалд гүдгэр гэнэ.
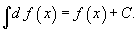
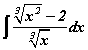интеграл бод
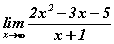хязгаарыг бод.
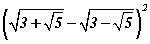утгыг ол.