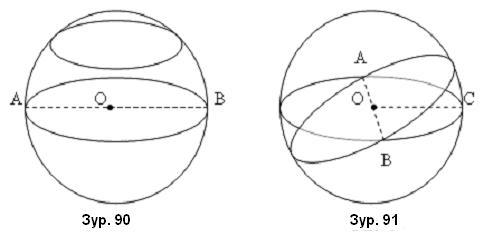
Бөөрөнхий гадаргуу гэдэг нь огторгуйд байрлах O гэсэн нэг цэгээс ижил зайд орших цэгүүдийн олонлог / цэгийн геометр байрлал / юм. O цэгийг бөөрөнхий гадаргуун төв гэнэ. /Зур. 90/ AO радиус, AB диаметрийг тойрог дээрхтэй адилаар тодорхойлно.
Бөөрөнхий гадаргуугаар хязгаарлагдсан биетийг шаар /бөмбөлөг/ гэнэ. Шаарын бүх хавтгай зүсэлт нь дугуй байна. /Зур. 90/ Хамгийн том дугуй нь шаарын төвийг дайрсан зүсэлтээр үүсэх бөгөөд том дугуй гэж нэрлэнэ. Дурын хоёр том дугуй шаарын диаметрээр огтлолцоно. /Зур. 91/ Шаарын диаметрын төгсгөлд байрлах хоёр цэгийг дайруулан хязгааргүй олон том дугуй татаж болно.
Архимедын теорем
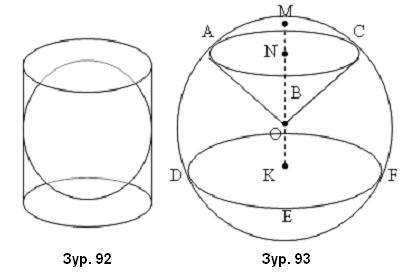
Цилиндрт багтсан шаарын эзэлхүүн цилиндерийн эзэлхүүнээс 1.5 дахин бага харин гадаргуун талбай нь цилиндерийн бүтэн гадаргуун талбайгаас 1.5 дахин бага байна. /Зур. 92/
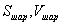 - шаарын гадаргуун талбай ба эзэлхүүн
- шаарын гадаргуун талбай ба эзэлхүүн 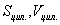 - цилиндрийн гадаргуун талбай ба эзэлхүүн гэвэл
- цилиндрийн гадаргуун талбай ба эзэлхүүн гэвэл
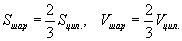
Шаарын хэсгүүд
Ямар нэгэн хавтгайгаар таслагдсан шарын хэсгийг ABC /Зур. 93/ шаарын сегмент гэнэ. ABC дугуйг шаарын сегментийн суурь, ABC дугуйн төв N -с бөөрөнхий гадаргуу хүртэлх MN хэрчмийг өндөр, M цэгийг орой гэнэ.
Бөөрөнхий гадаргуутай огтлолцсон ABC ба DEF гэсэн паралел хоёр хавтгайн дунд орших хэсгийг шаарын үе, шаарын үеийн муруй гадаргууг бүс /зон/ гэдэг. ABC ба DEF дугуйнуудыг шаарын бүсийн сууриуд, суурь хоорондын зай NK г өндөр гэнэ. AMCB бөөрнхий, OABC шовгор гадаргуунуудаар хязгаарлагдсан шаарын хэсгийг сектор гэдэг.





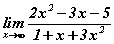 хязгаарыг тооцоол.
хязгаарыг тооцоол.
 функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол. тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.