Үндсэн ойлголт. Олонлогийн жишээ
Олонлог ба олонлогийн элемент гэдэг нь үгээр утга гаргасан тодорхойлолт байдаггүй суурь ойлголтуудад хамаарагдана. Иймээс тогтсон ерөнхий шинжтэй юмсын цуглуулгын талаар олонлог ба олонлогийн элемент гэсэн яриа үүснэ. Номын сангийн номууд, зогсоол дээрх автомашинууд, тэнгэрийн одод, дэлхийн ургамал амьтны аймаг гэх мэт нь бүгд олонлогийн жишээ юм.
Төгсгөлөг тоотой элементээс бүтсэн олонлогийг төгсгөлөг гэнэ. Жишээ нь: номын хуудас, сургуулийн сурагчид г.м
Нэг ч элементгүй олонлогийг хоосон гэнэ. Жишээ нь: далавчтай заануудын олонлог, sinx=2 тэгшитгэлийн шийдийн олонлог г.м
Материалыг тусгай эрхтэй хэрэглэгч үзнэ.
request_quoteТусгай эрх авах




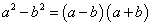 , кубуудын ялгавар
, кубуудын ялгавар 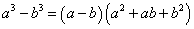 томьёонуудыг ихээр ашигладаг. Тэгвэл дөрөв, тав гэх мэтээр n зэргийн ялгаваруудад тохирох
томьёонуудыг ихээр ашигладаг. Тэгвэл дөрөв, тав гэх мэтээр n зэргийн ялгаваруудад тохирох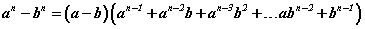
 тэгшитгэлийг бод.
тэгшитгэлийг бод.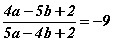 бол
бол 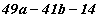 илэрхийллийн утгыг ол.
илэрхийллийн утгыг ол.