Тодорхой интегралыг математик, физик, механик, астроном зэрэг олон салбарт ашигладаг. Бид энд зөвхөн хоёр жишээ авч үзье.
Эргэлдэх биеийн эзэлхүүн
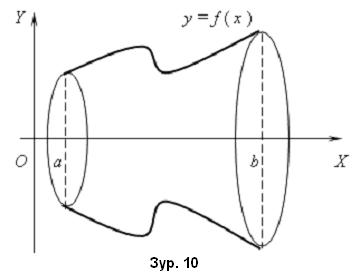
OX тэнхлэг, x=a, x=b шулуунууд, f(x) функцын графикаар хязгаарлагдсан муруй шугаман трапецыг OX тэнхлэгийг тойруулан эргүүлэхэд гарах биетийг авч үзье. /Зур. 10/
Эргэлдэх биеийн эзэлхүүн V нь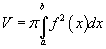 
тэнцүү.
Хувьсах хүчний ажил
OX тэнхлэгийн дагуу хөдлөх материаллаг цэгийг авч үзье. Цэг нь x тэнхлэг дээрх байрлалаасаа хамаарч f хүчээр хөдөлнө. Өөрөөр хэлбэл хүч нь x-ээс хамаарсан функц. Тэгвэл материаллаг цэгийг x=a байрлалаас x=b байрлалд шилжүүлэх ажил A нь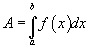 
гэсэн томьёогоор тодорхойлогдоно.
Жишээ
x=0, x=3 шугамуудаар хязгаарлагдасан y=x+1 шулуун OX тэнхлэгийг тойрон эргэлдэхэд гарах огтлогдсон конусын эзэлхүүнийг ол.
Бодолт
Дээр өгөгдсөн томьёогоор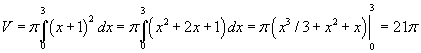 
болно.
үзэгдэл бүрт :
хос харш үзэдлүүдийн хувьд: 
тэнцэл биелнэ,
функцийн тодорхойлогдох мужийг ол.
-ийг ол.
хязгаарыг ол.