Бид хавтгайн геометрт нумын урт l, радиус r ба харгалзах өнцөг α -нууд нь α=l/r гэсэн харьцаатай байдгийг үзсэн. Энэ томьёо нь өнцгийн радиан хэмжээг тогтоох үндэс болно. Хэрвээ l=r бол α=1 болох бөгөөд энийг α өнцөг 1 радиантай тэнцүү гээд α=1 рад. гэж тэмдэглэнэ. Эндээс дараах тодорхойлолт гарна.
Нумын урт ба радиус нь тэнцүү төв өнцгийг радиан гэнэ. (AmB=AO) /Зур. 1/ Иймээс өнцгийн радиан хэмжээс гэдэг нь дурын радиусаар татаж гаргасан өнцгийн талуудын дунд орших нумын уртыг нумын радиуст харьцуулсан харьцааг хэлнэ.
Материалыг бүртгэлтэй хэрэглэгч үзнэ.
how_to_regБүртгүүлэх




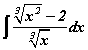 интеграл бод
интеграл бод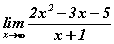 хязгаарыг бод.
хязгаарыг бод.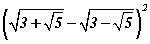 утгыг ол.
утгыг ол.