Нийлбэрийн шинжүүдийг сурагчид сайн мэддэг. Хүмүүс тоонуудын нийлбэрийг хурдан тооцоход эдгээр шинжүүдийг тогтмол хэрэглэдэг ч яг ямар шинж гэдгийг төдийлөн мэдээд байдаггүй.
Нийлбэрийн шинжүүд
Нийлбэр гэдэг бол хоёр ба түүнээс тоонуудыг нэг тоо болгон нэгтгэх арифметик үйлдэл.
Нийлбэрт орж буй тоонуудыг нэмэгдхүүн харин тэдгээрийг нэгтгэсэн тоо буюу үр дүнг нийлбэр гэж гэж нэрлэнэ. Нийлбэр дараах шинжүүдтэй.
Байр солих шинж
Нэмэгдхүүнүүдийн байрыг солиход нийлбэр өөрчлөгдөхгүй шинжийг бүгд мэддэг. Өөрөөр хэлбэл нийлбэрт орж буй гишүүдийн байрыг солиход нийлбэрт нөлөөлөхгүй гэсэн үг. Эндээс дурын a, b тоонууд эсхүл илэрхийллийн хувьд a+b=b+a байна.
Жишээ нь
6+7=7+6=13;
x2+3y+z=3y+z+x2;
1+2+3=3+2+1=6.
Бүлэглэн нэгтгэх шинж
Гурав ба түүнээс дээш нэмэгдхүүнтэй нийлбэрийн дурын нэмэгдхүүнүүдийг тэдгээрийн нийлбэрээр солиход нийлбэр өөрчлөгдөхгүй. Иймээс дурын a, b, c тоонууд эсхүл илэрхийллийн хувьд a+b+c=a+(b+c)=b+(a+c) байх болно.
Жишээ нь
6+7+3=6+(7+3)=6+10=16;
2x+3y+3x+2y=2x+3x+3y+2y=5x+5y;
2+13+8+7=2+8+13+7= (2+8)+(13+7)=10+20=30
Нэмэгдхүүнүүдийг тэдгээрийн нийлбэрээр солихын өмнө байр солих шинжийг ашиглаад дараа нь нэмэгдхүүнүүдийг тэдгээрийн нийлбэрээр сольж байгааг анхаарна уу. Тоонуудын хувьд бүлэглэн нэгтгэх шинжийг шууд ашиглаад явахад онцын хүндрэлгүй ч илэрхийллийн хувьд эхлээд байр солих шинжийг ашиглааад дараа нь бүлэглэх нь илүү оновчтой.
Шинжийг нийлбэрийг хурдан тооцоход ихээр ашигладаг.
Нийлбэр дэх тэг
Нийлбэрт орсон тэг нийлбэрт нөлөөлөхгүй. Эндээс a, b, 0 тоонууд эсхүл илэрхийллийн хувьд a+b+0=a+b=b+a байх болно.
Жишээ нь
6+2+0=8;
2x+3y+0=2x+3y=3y+2x;
Жич: Хичээлийн материал энгийн мэт санагдаж магадгүй. Сайтын материалууд ямарч насны, ямарч бэлтгэлтэй хүмүүст зориулагдсан тул агуулгын хувьд янз бүр байж таарна. Нийлбэрийн шинжүүдийг мэддэг хүнд энгийн боловч алгебрийг үзэж эхлэхдээ энгийн мэт эдгээр шинжүүдийг сайн ойлгон тогтоон авахгүйгээр өнгөрсөөр цааш илүү нарийн ухагдхуунуудыг ойлгохгүй болох суурь болдог гэдгийг санаарай.
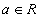энэ бичлэг нь a нь R олонлогийн элемент ба энэ олонлогт харьяалагдана гэснийг илэрхийлнэ. Эсрэгээр a нь R олонлогт харьяалагдахгүй гэдгийг 
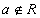гэж бичнэ.
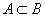гэж бичнэ. Дурын A олонлогийн хувьд 
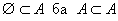багтаалт хүчинтэй.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.