Дөрвөн өнцөгт гэдэг нь дөрвөн өнцөг, дөрвөн талтай гүдгэр олон өнцөгт. Дөрвөн өнцөгтийг дөрвөн цуваанаас бүрдсэн битүү тахир шугамаар үүсэх хавтгайн тахир шугам доторх хэсэг бүрдүүлдэг.

Дөрвөн өнцөгтийг түүний оройг тэмдэглэсэн үсгүүдийн дарааллаар тэмдэглэнэ. Жишээ нь ABCD дөрвөн өнцөгт. Зурагт үзүүлсэн ABCD дөрвөн өнцөгтөд A, B, C, D - цэгүүд нь дөрвөн өнцөгтийн оройнууд харин AB, BC, CD, DA - бол түүний талууд.
Нэг тал дээр орших оройнуудыг хөрш, хөрш бус оройнуудыг эсрэг орших орой гэдэг.
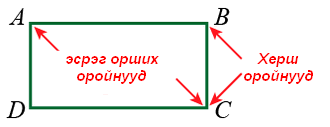
ABCD дөрвөн өнцөгтөд A ба B, B ба C, C ба D, D ба A оройнууд хөрш харин A ба C, B ба D оройнууд эсрэг орших оройнууд болно. Хөрш оройнуудын өнцгийг хөрш харин эсрэг орших оройн өнцгийг эсрэг орших гэж бас нэрлэдэг.
Дөрвөн өнцөгтийн талуудыг ч бас хөрш болон эсрэг орших гэж хувааж болно. Ерөнхий оройтой талуудыг хөрш эсхүл хамар харин ерөнхий оройгүй талуудыг эсрэг орших талууд гэж нэрлэдэг.
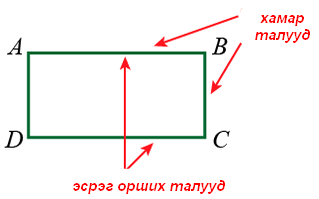
AB ба BC, BC ба CD, CD ба DA, DA ба AB - талууд хамар харин AB ба DC, AD ба BC - талууд эсрэг орших талууд.
Эсрэг орших оройнуудыг холбосон хэрчмийг дөрвөн өнцөгтийн диагонал гэдэг. Дөрвөн өнцөгтөд эсрэг орших хоёр хос оройнууд байдаг учраас түүнд хоёр диагонал байдаг.
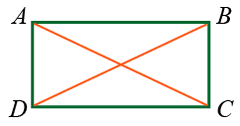
AC, BD хэрчмүүд нь ABCD дөрвөн өнцөгтийн диагоналууд.
Дөрвөн өнцөгтийн төрлүүд
Гүдгэр дөрвөн өнцөгтүүдийн үндсэн төрлүүдийг авч үзье.
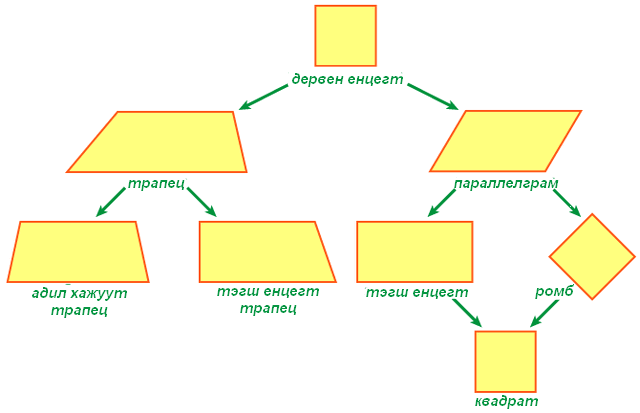
Трапец - эсрэг орших талуудын нэг хос нь бие биедээ паралел харин нөгөө хос нь паралел биш дөрвөн өнцөгт.
- Адил хажуут трапец -хажуу талууд нь тэнцүү трапец
- Тэгш өнцөгт трапец - аль нэг өнцөг нь тэгш өнцөгт трапец
Параллелграм - эсрэг орших талуудын хоёр хос бие биедээ паралел дөрвөн өнцөгт.
- Тэгш өнцөгт - бүх өнцөг нь тэнцүү параллелграм
- Ромб - бүх талууд нь тэнцүү параллелграм
- Квадрат - тал болон өнцгүүд нь тэнцүү параллелграм. Тэгш өнцөгт болон ромб квадрат байж болно.
Гүдгэр дөрвөн өнцөгтийн өнцгийн шинжүүд
Бүх гүдгэр дөрвөн өнцөгтийн өнцгүүд дараах шинжүүдтэй
- Дотоод ямарч өнцөг 180 градусаас бага
- Дотоод өнцгүүдийн нийлбэр 360 градустай тэнцүү.
Жич: Зарим сурагчдад хичээлийн материал энгийн санагдаж байж магадгүй. Гэхдээ сурагч бүр ижил төвшинтэй байдаггүй, сэдвийг дөнгөж судалж эхэлж байгаа гэх мэтээр бүхий л сурагчдад зориулж байгаа учраас зарим хичээлийн материал маш энгийн байх ч тохиолдол бий. Хэрвээ та хичээлийн материалыг мэдэж байвал их сайн. Хичээлд тайлбарлаад байгаа тодорхойлолтуудаар бодлогын нөхцлийг өгдөг учраас эдгээрийг цээжээр мэддэг байх хэрэгтэй. Жишээ нь бодлогын нөхцөлд эсрэг эсхүл хамар өнцгүүд гээд ороод ирэхэд юуг хэлээд байгааг мэдэхгүй бол зургийг гаргахад хүндрэнэ. Энэ нь бодлогыг шийдэж чадахгүйд хүргэх үндсэн шалтгаан болдог.





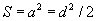
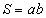
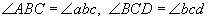 гэх мэт байна.
гэх мэт байна.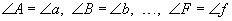 , харин талууд нь порпорционал байна.
, харин талууд нь порпорционал байна.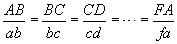
 илэрхийллийг хялбарчил.
илэрхийллийг хялбарчил.
 задаргааны 6-р гишүүнийг ол.
задаргааны 6-р гишүүнийг ол.