Бутархай хэсэгт зарим тоонууд хязгааргүй давтагдсан бутархайнууд байдаг. Ийм бутархайнуудын бичлэг 0,666666...; 1,33333...; 0,6818181818... гэж харагдах бөгөөд эдгээрийг үет бутархай гэж нэрлэдэг. Хичээлээр ийм бутархайнууд хэрхэн үүсдэг тэдгээртэй яаж ажиллахыг үзэх юм.
Үет бутархай үүсэх.
1-ийг 3 хуваавал эхлээд тэгээр өгөөд нэг үлдэнэ. Үлдэгдэл дээр тэг нэмээд 3 -аар өгөөд дахиад 1 үлдэнэ. Дахин тэг нэмээд 3-аар өгөөд дахиад нэг үлдэнэ. Эндээс 1:3=0,33333... гэсэн бутархай үүснэ.
Материалыг тусгай эрхтэй хэрэглэгч үзнэ.
request_quoteТусгай эрх авах
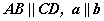бичлэгийг AB шулуун CD шулуунтай паралел, a шулуун b шулуунтай паралел гэж уншин ойлгож сураарай.
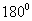. Зөрсөн AB ба CD /Зур. 70/ хоёр шулууны хоорондын өнцгийг дараах байдлаар тодорхойлно. 
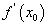, аргументын өөрчлөлт 
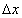ийн үржвэрийг функцын дифференциал гэнэ.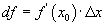 
n төрлийн обьект байлаа гэж үзье. Зургийг хар. Энд обьектудыг төлөөлүүлэн ердөө 3 төрлийн дүрсээр жишээ авъя. Эдгээр дүрсүүд дээр сэлгэмэл, гүйлгэмэл, хэсэглэл гэсэн ухагдхууныг авч үзнэ. Нийт обьектын тоо энд нэг их чухал биш гол утга учир ялгааг ойлгох нь чухал. Ухагдхууны ялгааг сайн ойлгоогүйгээс болоод ихэнх сурагчид ийм төрлийн бодлогыг бодохдоо хүндрэлтэй тулдаг.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.