Энгийн бутархайн үйлдлүүд

Бутархайг өргөтгөх.

Бутархайн хүртвар ба хуваарийг 0 -ээс ялгаатай тоогоор үржүүлбэл бутархайн утга өөрчлөгдөхгүй. Энэ хувиргалтыг бутархайг өргөтгөх гэнэ. Жишээ нь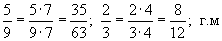



Бутархайг хураах.

Бутархайн хүртвар ба хуваарийг 0 -ээс ялгаатай тоонд хуваалбал бутархай өөрчлөгдөхгүй. Энэ үйлдлийг бутархайг хураах гэнэ. Жишээ нь

Материалыг бүртгэлтэй хэрэглэгч үзнэ.

how_to_regБүртгүүлэх

Мэдээлэл таалагдсан бол найзуудтайгаа хуваалцаарай.

Холбоотой материалууд
Гайхамшигт хязгаарыг ашиглах

  Нээгдсэн тоо: 17561 Нийтийн

Хязгаарыг бодох аргууд сэдвээр дахин нэг хичээлийг танилцуулж байна. Энд бид хязгаарыг бодоход гайхамшигт хязгаарыг хэрхэн ашиглах талаар авч үзэх юм. Гайхамшигт хязгаар цөөн тооны байдаг ч оюутан сурагчдад ихэнхдээ нэг ба хоёрдугаар гайхамшигт хязгаарыг ашигладаг. ЕБС-ын хэмжээнд гайхамшигт хязгаарын талаар дэлгэрэнгүй үзээд байдаггүй ч эдгээрийг мэдэж байх нь зарим төрлийн бодлогыг бодолтонд маш хэрэгтэй болдог. Хичээлийг материалыг судлахаасаа өмнө Хязгаарыг ойлгох нь, Хязгаарыг бодох аргууд хичээлүүдийг үзэж судалсан байхыг сануулъя.

Тригнометрийн бодолтын жишээ

  Нээгдсэн тоо: 2784 Төлбөртэй

Энэ нийтлэлээр бодит шалгалт дээр ирж байсан тригнометрийн хоёр бодлогын бодолтыг дэлгэрэнгүйгээр тайлбарлах болно. Эдгээр бодлогын бодолтыг сайн судлаад ойлговол тригнометрийн бодлогыг ойлгоход сайн суурь болж чадна. Бодлогын шийдүүдээс өгөгдсөн завсар дахь утгуудыг сонгох нэмэлт нөхцөл оруулсан нь сурагчдаас тригнометрийн илүү нарийн ойлголтыг шаардах юм. Сурагчид бодлогыг хураангуйлан энгийн хэлбэрт оруулж чаддаг ч шийдийг гаргах тэр тусмаа өгөгдсөн завсарт харьяалагдах шийдийг сонгохдоо үндсэн хүндрэлтэй тулдаг. Иймд бодолтуудыг анхааралтай судлаад ойлгон авахыг хичээгээрэй. Олон бодлого бодохдоо биш аргачлалыг ойлгох нь чухал.

Тэнцэл бишийг графикаар бодох

  Нээгдсэн тоо: 1794 Төлбөртэй

Нэг болон хоёр үл мэдэгдэгчтэй тэнцэл биш, тэнцэл бишийн системүүдийг функцын графикаар ойролцоогоор бодож болдог. Нэг үл мэдэгдэгчтэй тэнцэл бишийг бодохдоо бүх гишүүдийг тэнцэл бишийн нэг талд гарган f ( x ) > 0  хэлбэрт оруулаад f ( x ) = 0 функцын графикийг байгуулна. Үүний дараа графикийг ашиглан функцын тэгүүдийг олно. Эдгээр нь X тэнхлэгийг хэд хэдэн хэсэгт хуваасан байх бөгөөд x-ийн аль хэсэгт функцын утга тэнцэл бишийн утгатай давхцаж байгааг тодорхойлно.
Жишээлбэл: функцын тэгүүд нь a,b /Зур. 30/ гэе. Тэгвэл графикаас f ( x ) > 0 байх хэсэг нь x<a ба x>b гэдэг нь тодорхой. Эдгээр хэсгийг тодруулсан байгаа. Энд > тэмдгийн оронд <,  ≤, ≥ тэмдгүүдийн аль нь ч байж болно.

Нийлбэр ба ялгавар

  Нээгдсэн тоо: 3947 Бүртгүүлэх

Эерэг тоонуудын хувьд нэмэх, хасах үйлдлүүд энгийн боловч алгебрт эерэг, сөрөг тоонууд ойлголт орж ирснээр нэмэх хасах үйлдэл сурагчдыг ихээр сандралд оруулдаг. Энд хэдэн дүрмийг сайн ойлгоход л бүх зүйл хэвийн болно.

Үйл явдал…

Үйл явдал /event/ тодорхой үйлдэл хийгдсэн талаар системд мэдэгддэг. Хэрвээ бид энэхүү үйлдлийг ажиглах хэрэгтэй бол яг энд…

Нээгдсэн тоо : 316

 
Холбоосын параметрүүд

Манай төсөл олон хуудсуудтай болон тэдгээрийн хооронд динамикаар шилжилт хийж байгаа ч тухайн үед шилжилт хийгдсэн хуудаст тохирох…

Нээгдсэн тоо : 413

 
Зочин (Visitor)

Зочин (Visitor) паттерн классуудыг өөрчлөхгүйгээр тэдгээрийн обьектуудын үйлдлийг тодорхойлох боломжийг олгоно. Зочин хэвийг ашиглахдаа классуудын хоёр ангилалыг тодорхойлно.…

Нээгдсэн тоо : 362

 
Лямбда

Лямбда-илэрхийлэл нь нэргүй аргын хураангуй бичилтийг илэрхийлнэ. Лямбда-илэрхийлэл утга буцаадаг, буцаасан утгыг өөр аргын…

Нээгдсэн тоо : 458

 
Outlet компонент

Кодийн сайжруулалт /рефакторинг/ хичээлээр програмийн кодоо react -ийн зарчимд нийцүүлэн компонентод салгасан.…

Нээгдсэн тоо : 533

 
Хадгалагч (Memento)

Хадгалагч (Memento) хэв обьектын дотоод төлвийг түүний гадна гаргаж дараа нь хайрцаглалтын зарчмыг зөрчихгүйгээр обьектыг сэргээх боломжийг олгодог.

…

Нээгдсэн тоо : 527

 
Нэргүй арга

Делегаттай нэргүй арга нягт холбоотой. Нэргүй аргуудыг делегатийн хувийг үүсгэхэд ашигладаг.
Нэргүй аргуудын тодорхойлолт delegate түлхүүр үгээр…

Нээгдсэн тоо : 635

 
Урвуу матриц

Математикт харилцан урвуу тоонууд гэж бий. Ямар нэгэн тооны урвуу тоог олохдоо тухайн тоог сөрөг нэг зэрэг дэвшүүлээд…

Нээгдсэн тоо : 735

 
Кодийн сайжруулалт

Төсөлд react-router-dom санг оруулан чиглүүлэгчдийг бүртгүүлэн тохируулсан Санг суулган тохируулах хичээлээр бид хуудас…

Нээгдсэн тоо : 766

 
Энэ долоо хоногт
Бодлого 2.110

илэрхийллийг хялбарчил.

Нээгдсэн тоо : 755

 
Бодлого 2.116

Нээгдсэн тоо : 813

 
Бодлого 8.122

Задаргааны сүүлээсээ 3 дахь гишүүний бином коэффициент 45 бол задаргааны 6-р гишүүнийг ол.

Нээгдсэн тоо : 664

 
© 2014 Зохиогчийн эрхээр хамгаалагдсан. Холбогдох - 96655195