Бүхэл тоо гэдэг нь бутархай хэсэггүй эерэг ба сөрөг тоонууд болон тэг тоо юм. 0 нь эерэг ч биш сөрөг ч биш бүхэл тоо. Иймээс тэгийн өмнө ямар нэгэн тэмдэг тавих нь утга илэрхийлэхгүй +0, -0 бичлэг 0 бичлэгтэй ижил.
Эерэг ба сөрөг тоонууд
Тоолол нь хоёр эсрэг чиглэлд хийгддэг хэмжээсүүд байдаг. Жишээ нь дулааны хэм буюу температурийн тооллыг хоёр эсрэг чиглэлд хийдэг.
Жишээ нь хэмийн /температур/ тоололыг мөс хайлах хэм буюу буюу тэг хэмээс хоёр эсрэг тийш тоолдог. Хэм хэмжигчийг аваад үзье.
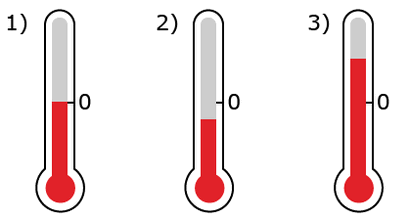
- Тэг хэм дэх мөнгөн усны түвшин. (мөс хайлах хэм).
- Тэгээс доош хэм дэх мөнгөн усны түвшин.
- Тэгээс дээш хэм дэх мөнгөн усны түвшин.
Эндээс тоолол нь хоёр эсрэг чиглэлд хийгдэх ямар нэгэн хэмжээс байвал ямар байх нь хамаагүй аль нэг чиглэлийг эерэг нөгөөг нь сөрөг гэж нэрлэдэг.
Эерэг тоо гэдэг нь тоололын эерэг чиглэлд хийгдсэн хэмжээсээр гарсан үр дүн юм. Эерэг тоог нэмэх (+) тэмдэгтэй тоогоор илэрхийлнэ. Жишээ нь +16, +20, +5 бол эерэг тоонууд
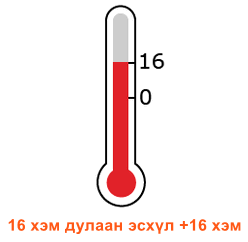
Хамгийн бага эерэг бүхэл тоо бол нэг (1).
Сөрөг тоо гэдэг нь тоололын сөрөг чиглэлд хийгдсэн хэмжээсээр гарсан үр дүн юм. Сөрөг тоог хасах (-) тэмдэгтэй тоогоор илэрхийлнэ. Жишээ нь -16, -21, -1 бол сөрөг тоонууд
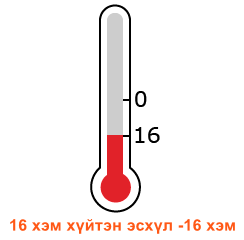
Хамгийн их сөрөг бүхэл тоо бол хасах нэг (-1).
Тэгээс бусад өмнөө (+) нэмэх тэмдэгтэй бичигдсэн тоонууд эерэг харин (-) хасах тэмдэгтэй бичигдсэн тоонууд сөрөг тоонууд байна.
Жишээ нь
+1, +15, +57 гэх мэтээр - эерэг тоонууд
-1, -15, -57 гэх мэтээр - сөрөг тоонууд
Эерэг тооны өмнө нь (+) тэмдэг тавин тэмдэглэж болохоос гадна түүний тавихгүй байсан ч бас болно. Өмнөө ямар нэгэн тэмдэггүй тоог эерэг тоо гэж үздэг. Жишээ +8, +14, +100 -гийн оронд 8, 14, 100 гэж бичиж болно.
Бүхэл тоонуудыг харьцуулах
Хоёр бүхэл тоог харьцуулна гэдэг нь тэдгээрийн аль нь их эсхүл бага эсхүл тоонууд тэнцүү гэдгийг тогтоох юм. Бүхэл тоонууд тоон цуваанд зүүнээс баруун тийш багаасаа их руу чиглэлтэй байрладаг тул тэдгээрийг тоон цуваагаар харьцуулж болно. Иймээс тоон цувааны таслалыг багын тэмдгээр солино гэсэн үг. Өөрөөр хэлбэл ... -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ... тоон цувааны таслалыг < тэмдгээр ... -5 < - <4 < -3 < -2 < -1 < 0 < 1 < 2 < 3 < 4 < 5 < ... солино.
Эндээс хоёр бүхэл тооны хувьд тоон цуваанд баруун тийш байрласан нь их харин зүүн тийш байрлалтай нь бага байх болно. Эндээс дараах чанарууд гарч ирнэ.
- Тэгээс их дурын бүхэл эерэг тоо бүх сөрөг тоонуудаас их. 1 > 0; 15 > -16.
- Дурын сөрөг бүхэл тоо тэгээс бага. -7 < 0; -357 < 0.
- Хоёр сөрөг тооны хувьд бүхэл тоон цуваанд баруун байрлалтай нь их байна. -31 < -28.
Сөрөг тоонуудын харьцуулалтын гуравдахь чанарыг сурагчид эерэг тоотой холин андуурах гээд байдаг. Өөрөөр хэлбэл -31 > -28 гэж үзэх гэдэг. Энэ бол буруу тоон цуваанд тоонууд ... -31, -30, -29, -28 ... буюу -28, -31 -ээс баруун байрлаж байгаа тул -31 < -28 байх ёстой.





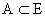 үзэгдэл бүрт :
үзэгдэл бүрт :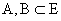 хос харш үзэдлүүдийн хувьд:
хос харш үзэдлүүдийн хувьд: 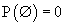 тэнцэл биелнэ,
тэнцэл биелнэ,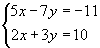 тэгшитгэлийн системийг бод.
тэгшитгэлийн системийг бод. тэгшитгэлийг бод.
тэгшитгэлийг бод.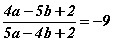 бол
бол 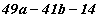 илэрхийллийн утгыг ол.
илэрхийллийн утгыг ол.