Пифагорийн теорем бол геометрийн бодлогод хамгийн ихээр ашиглагддаг теорем тул ихэнх сурагчид теоремийг сайн мэддэг. Хичээлээр теоремийн баталгаа болон Пифагорийн урвуу теоремийн талаар авч үзье. Пифагорийн теоремийн баталгааг мэдэж байх шаардлага байхгүй ч танин мэдэхүй болон ерөнхий мэдлэгийн хүрээнд танилцан ойлгох нь чухал. Энэхүү теоремийг их сургуулийн математикийн ангийн оюутнуудаар батлуулах даалгавар өгөхөд ихэнх нь чадахгүй байсан тохиолдол байдаг л юм даа.
Зөвлөмж: Ирээдүйд сургалтын үндсэн арга онлайн буюу интернет технологт суурилана гэдэг нь нэгэнт тодорхой болсон. Теле болон DVD, Flash гэх мэт зөөгч дээрх хичээлүүд өгөөж сайнгүй гэдгийг сүүлийн хоёр жил харуулсан. Хичээлийг судлан Пифагорийн теоремийн баталгааны ерөнхий логикийг ойлгож чадвал та онлайн сургалтаар өөрийгөө хөгжүүлэх боломж байна гэж үзээрэй. Нэг үзээд ойлгохгүй бол дахиад үзээрэй. Эцэст нь хичээлийн материалийг бүрэн ойлгоно гэдэгт бүү эргэлзээрэй. Материалийг бүрэн ойлгосны дараа Пифагорийн теоремийг өөр аргаар батлах гээд оролдоорой.
Пифагорийн теорем
Тэгш өнцөгт гурвалжны гипотенузийн квадрат катетуудын квадратуудын нийлбэртэй тэнцүү. Математикийн хэлээр бол
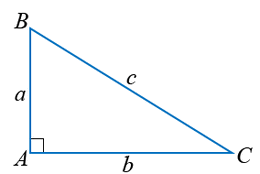
Хэрвээ өнцөг A=900 бол a2+b2=c2 гэсэн үг.
Баталгаа
a, b катетуудтай c гипотенузтай тэгш өнцөгт
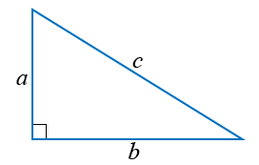
гурвалжинг авч үзье. Дээрх гурвалжинг нэмэлт байгуулалтаар a+b талтай квадрат болгон
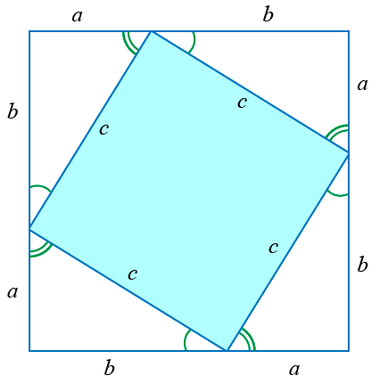
өргөжүүлье. Энэхүү квадратийн талбай S=(a+b)2 байх нь ойлгомжтой. Нөгөө талаас дээрх квадрат ab/2 талбайтай дөрвөн ижилхэн гурвалжин c талтай квадратаас бүрдэнэ. Эндээс квадратийн талбай
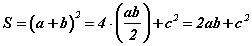буюу 
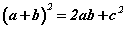
болно гэсэн үг. Нийлбэрийн квадратийн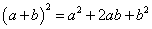 
томьёогоор 
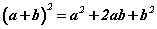гэдгээс дээрх тэнцэл 
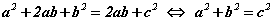болсноор теорем батлагдана.
Пифагорийн урвуу теорем
Гурвалжны нэг талын квадрат нь нөгөө хоёр талынхаа квадратуудын нийлбэртэй тэнцүү бол гурвалжин тэгш өнцөгт байна. Математикийн тодорхойлолтоор бол
Хэрвээ a2+b2=c2 бол ABC гурвалжин тэгш өнцөгт байна.
Баталгаа
a2+b2=c2 байх a, b, c талуудтай ABC гурвалжны
өнцөг A=900 гэдгийг батлая. Үнний тулд A1=900 , A1B1=a, A1C1=b -тэй тэнцүү
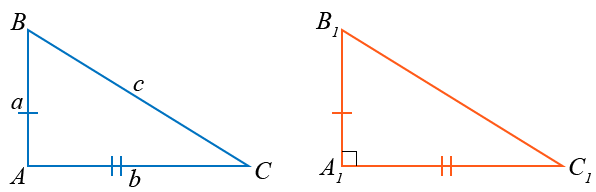
A1B1C1 гурвалжинг авч үзье. Пифагорийн теоремоор A1B1C1 гурвалжны хувьд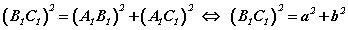 
байх ёстой. Харин Пифагорийн теоремийн тодорхойлолтоор a2+b2=c2 бөгөөд эндээс 
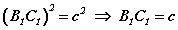гэсэн дүгнэлтийг хийж болно. Иймээс ABC , A1B1C1 гурвалжингуудын гурван талууд тэнцүү тул 
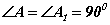буюу ABC гурвалжин тэгш өнцөгт гэдэг нь батлагдана.
Хүсэлт: Хичээл танд таалагдсан бол нийтийн сүлжээний логоний зурагт дээр даран бусдад тараахыг хичээнгүйлэн хүсье.
гэсэн P1 цэгээр илэрхийлэгдэх хувиргалт юм.
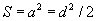
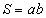
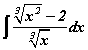интеграл бод
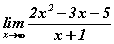хязгаарыг бод.
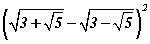утгыг ол.