Тоо гэдэг ухагдхууныг хүмүүс маш эртнээс бий болгон ашиглан ирсэн. Эхлээд натурал тооны олонлог бий болон араас нь бутархай, эерэг иррационал тоонууд бий болсон. Орчин үеийн математикт тоонуудыг олон дэд олонлогт задлан үзэх болсон. Сурагчид эдгээр тоон олонлогуудын талаарх мэдлэг дутуугаас зарим нэгэн тэмдэглэгээг ч мэдэхгүй байх нь элбэг. Тоонуудын олонлогийн талаар сайн ойлгон тухайн олонлогт ямар тоонууд ордогийг мэдэж байх хэрэгтэй. Олонлогт багтах тоонуудыг сурагчид бараг бүгд мэддэг хирнээ ямар олонлог, хэрхэн тэмдэглэдэг, ямар шинжүүдтэй зэргийг мэддэггүй. Үүнээс болоод зарим бодлогын нөхцлийг буруу ойлгох, шийдийн олонлогийг буруу бичих зэрэг алдаануудыг гаргадаг. Иймээс тоон олонлогуудыг талаар мэдлэгтэй болцгооё.

Натурал тоо N.

Натурал тооны олонлогийг N={1,2,3,4 ...} гэж тэмдэглэдэг бөгөөд хааяа түүнд тэгийг нэмэн N₀ гэж тэмдэглэнэ. Натурал тооны олонлогийн дурын 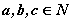тоонуудын хувьд нэмэх (+), үржих (*) үйлдэлд

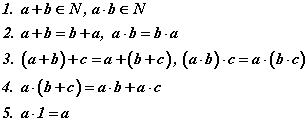
шинжүүдийг тодорхойлсон байдаг. Натурал тоон олонлог үржих, нэмэх үйлдэлийн хувьд битүү байдаг. Өөрөөр хэлбэл ямарч натурал тоонуудыг хооронд нэмэх эсхүл үржихэд үр дүнд нь натурал тоо л гарна гэсэн үг. Байр солих, бүлэглэх, тэгээр үржих дүрмүүдийг хүмүүс сайн мэддэг. Нэмэх, үржих үйлдлүүдээс гадна натурал тооны олонлогийн дурын 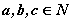тоонуудын хувьд бага (<), бага буюу тэнцүү ( ≤ ) харьцааг

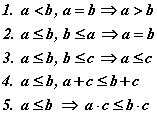[PICTURE math10_50_03.gif]

шинжүүдтэйгээр тодорхойлдог.

Бүхэл тоо Z

1, -20, 100, -100, 25, 30, -31 эдгээр нь бүхэл тоонууд.
a+x=b тэгшитгэлд a, b - тодорхой натурал тоонууд харин x - үл мэдэгдэх натурал тоо гэвэл тэгшитгэлийн бодолтонд шинээр хасах (-) үйлдлийг оруулах шаардлагатай. x=b-a тэгшитгэлийг хангах x натурал тоо байдаг гэвэл энэхүү тэгшитгэл заавал N олонлогт шийдтэй байх албагүй учраас натурал тоон олонлогийг өргөжүүлэх хэрэгцээ гарна. Эндээс Z={0, 1, -1, 2, -2, 3, -3 ...} буюу бүхэл тоон олонлог гарч ирнэ.
Натурал тоон олонлог бүхэл тоон олонлогт багтаж байгаа учраас натурал тоон олонлогийн нэмэх (+), үржих (*) үйлдлүүд бага (<), бага буюу тэнцүү ( ≤ ) харьцаануудын шинжүүд Z олонлогт хүчинтэй байхын дээр

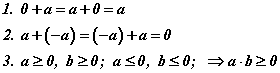
дээрх шинжүүд нэмэгдэнэ.

Рационал тоо Q

a·x=b тэгшитгэлийг авч үзье. Энд a, b тодорхой бүхэл тоонууд харин x - үл мэдэгдэгч. Тэгшитгэлийг бодохын тулд хуваах (:) үйлдлийг оруулан ирвэл тэгшитгэлийн шийд 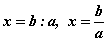болно. Эндээс x байнга бүхэл тоон Z олонлогт тодорхойлогдохгүй гэдэг нь ойлгомжтой. Иймээс бүхэл тоон олонлогийг өргөжүүлэх шаардлага үүссэнээр 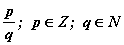элемент бүхий рационал тоон олонлог Q гарч ирдэг. q=1 гэвэл бүхэл тоо олонлог рационал тоон олонлогийн дэд олонлог буюу 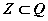болох тул өмнөх олонлогуудын бүх дүрмүүд Q олонлогт хүчинтэйн байхын дээр нэмэх, үржих үйлдлүүд энэ олонлогт

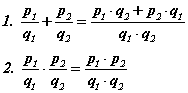
дүрмээр хийгдэн харин хуваах үйлдэлд

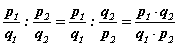
дүрэм үйлчилнэ.
a≠0 үед Q олонлогт a·x=b тэгшитгэл цорын ганц шийдтэй. Тэгд хуваалт тодорхойлогдохгүй. Эндээс Q олонлогт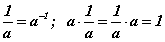
шинжтэй эсрэг элемент байдгийг тодорхойлно. Q олонлогт харьцуулалтын шинжийг 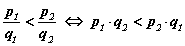гэж өргөтгөж болно.
Q олонлогийн хоёр тооны хооронд хязгааргүй олон рационал тоонууд байж болдог нэгэн чухал шинж бий. Иймээс Q олонлогт зэрэгцээ орших рационал тоонууд гэж байдаггүй нь натурал, бүхэл тоон олонлогоос ялгаатай.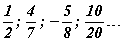
тоонууд бол рационал тоонуудын жишээ.

Иррационал тоо I

Дурын хоёр рационал тоонуудын хооронд хязгааргүй тооны өөр рационал тоонууд байж болно гэдгээс үүдэн рационал тоонууд маш нягт учраас түүнийг цааш өргөжүүлэх шаардлагагүй гэсэн алдаатай дүгнэлтийг хийхэд хүргэдэг. Бүр Пифагор ч өөрийн үедээ ийм алдааг хийж байсан. Гэсэн хэдий ч эрдэмтэд 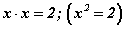тэгшитгэлийн шийдийг рационал тооны олонлогт судлахдаа алдаатай дүгнэлтийг няцаажээ. Ийм тэгшитгэлийг бодохдоо квадрат язгуур гэдэг ойлголтыг бий болгосноор тэгшитгэлийн шийд 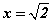хэлбэртэй болсон. a - тодорхой рационал тоо, x - үл мэдэгдэгч байх 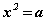хэлбэрийн тэгшитгэл рационал тооны олонлогт дандаа шийдтэй байдаггүйгээс үүдэн тооны олонлогийг өргөтгөх хэрэгцээ гарч ирснээр иррационал тоон олонлог үүссэн. 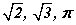зэрэг тоонууд иррационал тоон олонлогт харьяалагдана. Иррационал тооны жишээнүүд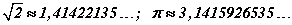

Бодит тоо R

Рационал ба иррационал тооны олонлогуудын нэгдэл бол бодит тоон олонлог юм. Рационал тоо олонлог бодит тоон олонлогт багтана гэдгээс түүнд хүчинтэй арифметик үйлдлүүд, харьцаанууд өөрийн шинжээ шинэ олонлогт хадгална гэж үзэж болохоор. Үүний баталгаа нь нилээд төвөгтэй учраас дээр дурдсан арифметик үйлдлүүд, харьцаануудын шинжүүдийг бодит тоон олонлогт аксиом байдлаар оруулдаг. Алгебрт ийм обьектыг талбар гэдгээс бодит тоон олонлогийг эрэмбэлэгдсэн талбар гэж үздэг.