Интеграл, уламжлал хоёр мат анализд голлох байр суурийг эзэлдэг тухай би өмнө нь Уламжлалыг тооцох хичээлд дурдаж байсан. Интегралыг олох үйлдлийг интегралчлах гэж нэрлэдэг. Хичээлийн материалыг сайн ойлгохын тулд та уламжлалыг олох наад захын болбол дунд хэмжээний мэдлэгтэй байх хэрэгтэй. Иймд эхлээд Уламжлалыг тооцох, Дифференциалчлах дүрэм хичээлийг үзэн судалсан байхыг зөвлөе. Интеграл үзэх гэж байж юун уламжлал яриад байгаад гайхаж магадгүй. Тэгвэл уламжлал олох (дифференциалчлах), тодорхойгүй интегралыг олох (интегралчлах) хоёр нь нэмэх, хасах эсхүл үржих, хуваахын адилаар харилцан эсрэг үйлдлүүд юм. Эндээс нэг үйлдлийг мэдэхгүйгээр /өөрөөр хэлбэл уламжлалыг олох дадлагагүйгээр/ нөгөөд нь хол явахгүй нь ойлгомжтой.
Үүнээс гадна бидэнд Уламжлалын үндсэн жагсаалтууд , Үндсэн интегралуудын жагсаалтуудын томьёонууд хэрэгтэй.
Тодорхойгүй интегралд юу нь хэцүү вэ? гэвэл дифференциалчлахад тогтсон 5 дүрэм, уламжлалын үндсэн жагсаалт гээд үйлдлийн нилээд нарийн алгоритм байдаг бол интегралд бүгд өөр интегралчлах хэдэн арван дүрэм үйлчилдэг. Гэхдээ бид үндсэн цөөн тооны дүрмийг, үндсэн интегралуудын жагсаалтуудтай ашиглаж сурсан байхад хангалттай.
Интегралын хүснэгтээс харвал уламжлалынхтай адилаар интегралчлах хэдэн дүрэм, зарим элементар функцийн интегралуудыг харна. Хүснэгтээс ямарч интеграл
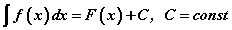 хэлбэртэй байгааг амархан харж болохоор. Энэ бичлэгийг нарийвчлан ойлгохоос эхлэе.
хэлбэртэй байгааг амархан харж болохоор. Энэ бичлэгийг нарийвчлан ойлгохоос эхлэе.
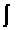 - интегралын тэмдэг.
- интегралын тэмдэг.- f(x) - интеграл доорх функц
- dx - дифферанциалын тэмдэг. Интегралын бичилт болон бодох үедээ энэ тэмдгийг орхиж болохгүй.
- f(x)dx - интеграл доорх илэрхийлэл
- F(x) - эх функц
- F(x)+C - эх функцийн олонлог. Энд тогтмолд их анхаарал өгөөд байх хэрэггүй. Ямарч тодорхойгүй интегралын хариунд C тогтмолыг нэмж өгдөг.
Интегралын бичилт болон хүснэгтийн интегралуудыг дахин харвал тэнцүүгийн тэмдгийн зүүн тал 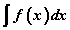 нь F(x)+C гэсэн өөр функц болоод байгаа биз.
нь F(x)+C гэсэн өөр функц болоод байгаа биз.
Эндээс 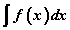 тодорхой бус интегралыг бодно гэдэг нь тодорхой дүрмүүд болон хүснэгтээ ашиглан түүнийг F(x)+C гэсэн тодорхой функцэд шилжүүлэх гэж тодорхойлж болно.
тодорхой бус интегралыг бодно гэдэг нь тодорхой дүрмүүд болон хүснэгтээ ашиглан түүнийг F(x)+C гэсэн тодорхой функцэд шилжүүлэх гэж тодорхойлж болно.
Интегралын хүснэгтээс жишээ болгоод 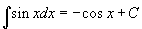 авъя. Энд интеграл гэж юу болох, эх функц юуг хэлэх гэсэн онолыг мэдээд байх шаардлага багатай. Яагаад
авъя. Энд интеграл гэж юу болох, эх функц юуг хэлэх гэсэн онолыг мэдээд байх шаардлага багатай. Яагаад 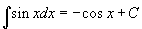 томьёоны хувьд
томьёоны хувьд 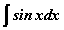 интеграл -cosx+C болон хувирч байгааг мэдэх албагүй. Ер нь интегралын хүснэгтийг өгөгдсөн томьёонууд гэж үзээд тогтоон авах нь зөв.
интеграл -cosx+C болон хувирч байгааг мэдэх албагүй. Ер нь интегралын хүснэгтийг өгөгдсөн томьёонууд гэж үзээд тогтоон авах нь зөв.
Дифференциалчлах, интегралчлах хоёр нь харилцан эсрэг үйлдлүүд гэдгээс ямарч эх функц зөв гарсан бол 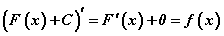 тэнцэл биелэгдэх ёстой. Өөрөөр хэлбэл зөв эх функцийг дифференциалчлахад интеграл доорх анхдагч функц гарах ёстой.
тэнцэл биелэгдэх ёстой. Өөрөөр хэлбэл зөв эх функцийг дифференциалчлахад интеграл доорх анхдагч функц гарах ёстой.
Тэгвэл 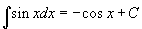 интегралд дээрх томьёо хүчинтэй эсэхийг шалгая. Интегралын баруун хэсгээс уламжлал авбал
интегралд дээрх томьёо хүчинтэй эсэхийг шалгая. Интегралын баруун хэсгээс уламжлал авбал 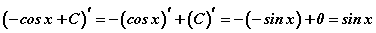 гээд интеграл доорх функц гарч ирж байна. Эндээс эх функц дээр яагаад C тогтмол нэмэгдээд байгаа нь ч тодорхой болж ирлээ. Эргээд уламжлал авахад тогтмолууд тэг болох тул эх функц хичнээн ч байж болох нь байна.
гээд интеграл доорх функц гарч ирж байна. Эндээс эх функц дээр яагаад C тогтмол нэмэгдээд байгаа нь ч тодорхой болж ирлээ. Эргээд уламжлал авахад тогтмолууд тэг болох тул эх функц хичнээн ч байж болох нь байна.
Иймээс тодорхойгүй интегралыг бодно гэдэг нь ямар нэг функцийг олох биш эх функцийн бүх олонлогийг олохыг хэлнэ. 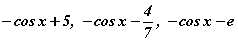 зэрэг бүх функцууд бидний авч үзсэн хүснэгтийн
зэрэг бүх функцууд бидний авч үзсэн хүснэгтийн 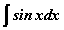 интегралын шийд болно.
интегралын шийд болно.
Тодорхойгүй интегралын үндсэн шинжүүд
- Тодорхойгүй интегралаас авсан уламжлал интеграл доорх функцтэй тэнцүү.
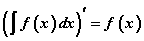
- Тодорхойгүй интегралын дифференциал интеграл доорх илэрхийлэлтэй тэнцүү.
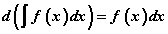
- Аливаа функцийн дифференциалын тодорхойгүй интеграл энэ функц болон дурын тотмолын нийлбэртэй тэнцүү
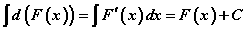
- Тогтмолыг интегралаас гаргах эсхүл оруулж болно
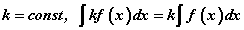
- Хоёр түүнээс дээш функцуудын нийлбэр, ялгаварын тодорхойгүй интеграл эдгээр функцуудын тодорхойгүй интегралын нийлбэр, ялгавартай тэнцүү
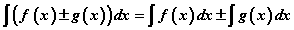
Энд нэг зүйлийг тодруулах хэрэгтэй. Бид уламжлал олохыг - дифференциалчлах, интегралыг олохыг - интегралчлах гэдгийг мэдсэн Тэгвэл интеграл доорх илэрхийлэлд байгаа dx -г дифферанциалын тэмдэг буюу дифференциал гэж нэрлээд байгаа. 2-р шинжид энэ тухай бас гарсан.
Тодорхойлолтын дагуу функцын уламжлал 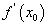 , аргументын өөрчлөлт
, аргументын өөрчлөлт 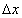 ийн үржвэрийг функцын дифференциал гэдэг бөгөөд
ийн үржвэрийг функцын дифференциал гэдэг бөгөөд 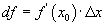 гэж үзэж болно. Их энгийнээр тайлбарлах гээд үзье.
гэж үзэж болно. Их энгийнээр тайлбарлах гээд үзье.
Шинэ хувьсагч оруулах арга нь интегралчлах үндсэн аргуудын нэг. Орлуулга хийгээд шинэ хувьсагч оруулан ирэхэд интеграл доорх функцийн dx (x- ийн дифференциал) шинэ хувьсагчийн дагуу функц агуулах болдог. Энэ үед дифференциалыг тооцох хэрэгтэй болдог.
Дифференциалыг нээх дүрэм
Дифференциал нээнэ гэдэг нь дифференциалд байгаа функцийн уламжлалыг олохыг хэлнэ. Өөрөөр хэлбэл d тэмдгийг араас хаалтанд байгаа илэрхийллийн уламжлалыг олоод илэрхийлэлд байгаа хувьсагчийн дифференциалаар үржин өгөх юм. Алхам бүрээр нь авч үзвэл
- d тэмдгийг арилгана
- хаалтны баруун дээр уламжлалын тэмдэгийг тавина
- илэрхийллийн ард dx үржигдхүүнийг нэмэн өгнө.
Жишээ нь 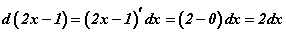 Цаашдаа интеграл бодоход маш хэрэгтэй болдог тул жишээтэй харьцуулаад сайн тогтоогоод аваарай.
Цаашдаа интеграл бодоход маш хэрэгтэй болдог тул жишээтэй харьцуулаад сайн тогтоогоод аваарай.





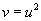 гэсэн функц байсан гэе. Энд u нь аргумент, v нь функц. Хэрвээ эдгээрийн үүргийг соливол v ээс хамаарсан u функц гарна.
гэсэн функц байсан гэе. Энд u нь аргумент, v нь функц. Хэрвээ эдгээрийн үүргийг соливол v ээс хамаарсан u функц гарна. 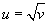
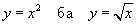 гэсэн нэг нь нөгөөдөө урвуу хоёр функц гарна.
гэсэн нэг нь нөгөөдөө урвуу хоёр функц гарна.
 задаргааны хамгийн их нэмэгдхүүн
задаргааны хамгийн их нэмэгдхүүн  бол a, b, c -г ол.
бол a, b, c -г ол. тэгшитгэлийг бод.
тэгшитгэлийг бод. функцийн уламжлалын
функцийн уламжлалын  утгыг ол.
утгыг ол.