Орой бүрд нь ижил тоотой талууд нийлдэг, бүх тал нь хоорондоо тэнцүү зөв олон өнцөгтөөс бүрдсэн олон талтыг зөв олон талт гэнэ.
Зөвхөн таван гүдгэр, дөрвөн гүдгэр биш зөв олон талт мэдэгдэж байгаа. Гүдгэр зөв олон талтууд:
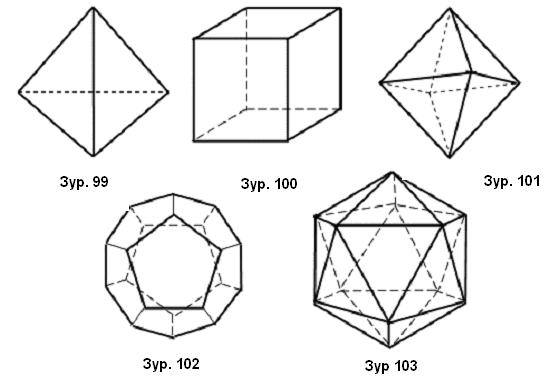
Дурын зөв олон талтад шаарыг багтааж болно. Мөн түүнчлэн тэдгээрийг шаарт багтааж болно.
Мэдээлэл таалагдсан бол найзуудтайгаа хуваалцаарай.
Нээгдсэн тоо: 593 Төлбөртэй
Математикийн бүх илэрхийллүүд хамгийн сүүлд хийгдэх үйлдлээрээ нэрлэгддэг. Үүнийг сайн тогтоон аваарай. Учир нь сурагчид илэрхийллийг хараад a дээр нэмэх b хасах нь c үржих нь d гэх мэтээр унших гээд байх нь элбэг. Энэ нь таны алгебрийн анхан шатны мэдлэггүй гэж үзэхэд хүргэх том асуудал болохыг сануулъя.
Иймээс хичээлээр илэрхийллийг хэрхэн зөв уншихыг сурцгаая.
Нээгдсэн тоо: 2195 Төлбөртэй
Өмнөх хичээлүүдээр бид ерөнхий үржигдхүүнийг хаалтнаас гаргах, бүлэглэх гэсэн хоёр аргыг сурсан. Энэ удаа үржүүлэхийн хураангуй томьёог ашиглах хүчирхэг аргатай танилцах болно. Үүнийг сурагч бүр мэднэ. Томьёонуудыг ч сайн мэднэ гэж бодож байна. Тэгвэл энэ тухай ярих хэрэг байгаа юм уу гэсэн асуулт гарч болох юм. Томьёонуудыг математикт маш өргөнөөр ашигладаг. Тэдгээрийг үржүүлэх, бутархайг эмхэтгэх, тэгшитгэл бодох, интеграл тооцох гээд хэрэглэхгүй газаргүй. Иймээс эдгээр томьёонууд хаанаас гарч ирсэн, юунд хэрэгтэй, хэрхэн тогтоох, яаж хэрэглэх гээд шуудхан хэлэхэд авч үзэх зүйлүүд байна аа. Сурагчид томьёог сайн цээжилсэн мөртлөө бодлого дээр очоод бараг мэдэггүй хүн шиг болдог. Өөрөөр хэлбэл ашиглах тал дээр ноотой.
Нээгдсэн тоо: 713 Нийтийн
Тэг тоонд нэгж байдаггүй тул түүнийг ямар нэгэн тоон дээр нэмэх эсхүл хасахад тухайн тоо өөрчлөгддөггүй.
Нээгдсэн тоо: 3802 Төлбөртэй
Өнцөг
Огтлолцсон хоёр шулууны хоорондох өнцгийг хавтгайн геометрийн адилаар хэмжинэ. Учир нь эдгээр шулууныг дайруулан хавтгай татаж болдог. Паралел хоёр шулууны хоорондын өнцөг нь 0 эсвэл 
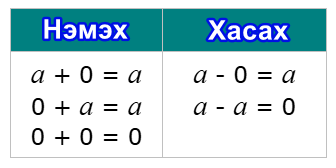
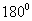. Зөрсөн AB ба CD /Зур. 70/ хоёр шулууны хоорондын өнцгийг дараах байдлаар тодорхойлно.
Дурын O цэгийг дайруулаад OM || AB ба ON || CD байх OM, ON цацрагийг татна. Тэгвэл AB ба CD гийн хоорондох өнцөг нь NOM тэй тэнцүү гэж үзнэ. Өөр хэлбэл AB ба CD шулууныг өөртөө нь паралел байдлаар огтлолцох хүртэл нь шилжүүлнэ гэсэн үг. Тухайлбал O цэгийг AB ба CD шулуунуудын аль нэг дээр авч болно. Энэ тохиолдолд O цэг нь хөдөлгөөнгүй байна.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
Нээгдсэн тоо : 746
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.