Нүүр » Математик » Үндсэн курс » Зарим тодорхой интегралууд

Зарим тодорхой интегралууд

Зарим тодорхой интегралууд



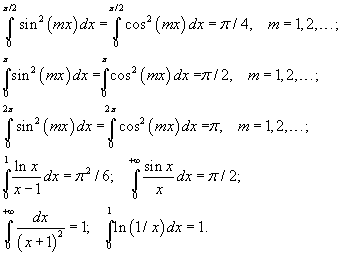
Хувьсах дээд хязгаартай интеграл

[a , b] хэрчимд f(x) тасралтгүй функц өгөгдсөн гэе. Тэгвэл дурын 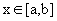хувьд

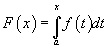
гэсэн хувьсах дээд хязгаартай интегралаар /тэнцлийн баруун хэсэг/ өгөгдсөн функц байна.
Хувьсах дээд хязгаартай интегралд тодорхой интегралын бүх шинж чанар хүчинтэй үйлчилнэ.

Жишээ
Шулуун зам дээр хувьсах хүч нь x≥0 үед f(x)=6x2+5 дүрмээр өөрчлөгддөг бол энэ хүчний ажил ямар дүрмээр өөрчлөгдөх вэ?

Бодолт
Шулуун замын [0 , x] хэрчимд f(x) хүчний ажил нь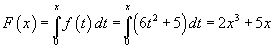
тэнцүү.
Тэгэхлээр ажил нь F(x)=2x3+5x дүрмээр өөрчлөгдөнө.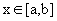
үед хувьсах дээд хязгаартай интегралын тодорхойлолт ба интегралын шинжээс 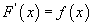гарна.

 

Мэдээлэл таалагдсан бол найзуудтайгаа хуваалцаарай.

Холбоотой материалууд

Функцын хязгаар

x нь a д тэмүүлэх үед дурын ε>0 хувьд нөхцлийг хангах ε тооноос хамаарсан δ(ε) тоо олдож байвал L тоог…

Нээгдсэн тоо : 3239

Зөв олон талт

Орой бүрд нь ижил тоотой талууд нийлдэг, бүх тал нь хоорондоо тэнцүү зөв олон өнцөгтөөс бүрдсэн олон талтыг зөв олон…

Нээгдсэн тоо : 4782

Тэгш хэм. Хавтгай дүрсүүдийн тэгш хэм

Биет дээр орших E цэг бүрт энэ биет дээр E’ гэсэн цэг олдоод EE’ хэрчим нь S хавтгайтай перпендикуляр бөгөөд…

Нээгдсэн тоо : 2059

Тодорхойгүй интеграл

Хэрвээ X хэсэгт байх x болгоны хувьд бол тасралтгүй F(x) функцыг f(x) ийн эх функц гэнэ.Жишээ(-∞,+∞) мужид функц нь учраас…

Нээгдсэн тоо : 2461