Модул орсон тэгшитгэл сурагчдыг хүнд асуудалд оруулдаг. Шалгалт шүүлэгт ийм төрлийн тэгшитгэлүүд дээр сурагчид ихэнх нь таах аргаар хариуг бөглөдөг нь нууц биш. Гэтэл тэтэгэлэгт хөтөлбөр, уралдаант шалгалт гэх мэт илүү нарийн авдаг буюу бичгийн шалгалтанд тааж оноо авна гэсэн ойлголт байхгүй болдог. Ялангуяа өгсөн даалгаварын бодолтоор оноо өгдөг бичгийн даалгавар байвал яах билээ. Иймээс сэдвийг онолын болоод практик талаас гүнзгий ойлгосон байх хэрэгтэй. Ингэж чадсан тохиолдолд шалгалт, шүүлэгийг ямарч хэлбэрээр авсан танд асуудал үүсэхгүй. Хичээлээр тэгшитгэлийн хоёр талд модул орсон болон модултай тэгшитгэлийг задлах аргаар бодох тухай үзнэ. Материалыг илүү сайн ойлгохын тулд Модултай тэгшитгэлийг бодох II , Модултай тэгшитгэлийг бодох I хичээлүүдийг үзсэн байхыг зөвлөе.
ЭЕШ -д 800 оноо, Хоцрогдлыг бүрэн арилгана гэх мэтийн таныг цоо шинэ хүн болгочих юм шиг лоозун бол худлаа зүйл гэдгийг нэг мөр ойлгон аваарай. Таны асуудал таных байхаас өөр хэнийх ч биш тул та өөрөө л хичээн зүтгэн, тэсвэр, тэвчээрээ гаргаснаар амжилтанд хүрнэ гэдгийг хүн төрөлхтний түүх хэзээний баталсан зүйл.
Материалыг тусгай эрхтэй хэрэглэгч үзнэ.
request_quoteТусгай эрх авах
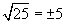Учир нь (+5)2=25 бас (-5)2=25 байдаг. 
интеграл бод
хязгаарыг бод.
утгыг ол.