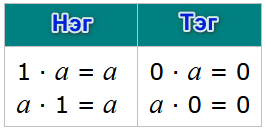
Нийлбэр дэх бүрдүүлэгчдийг нэгтгэн нэмэх дүрэм -ийг үндэслэн дараах хоёр дүрэм гарч ирдэгийг хичээл үзье.
Нийлбэрийн дүрэм, шинжүүдийг маш сайн ойлгон, ашиглаж сурах нь цаашид илэрхийллийн хувиргалт, хялбарчлалд их хэрэгтэй.
- Тоон дээр хоёр ба түүнээс дээш тоонуудын нийлбэрийг нэмэхдээ энэхүү тоон дээр нийлбэрийн дурын бүрдүүлэгчийг нэмээд гарсан үр дүн дээр дараагийн бүрдүүлэгчдийг нэмэх байдлаар тооцож болдог.
Жишээ нь 10 дээр 20 + 3 нийлбэрийг нэм.
Нийлбэрийг олохдоо дээрх дүрмээр 10 + (20 + 3) = (10 + 20) + 3 = 30 + 3 = 33 эсхүл 10 + (20 + 3) = (10 + 3) + 20 = 13 + 20 = 33 гэж тооцох боломжтой. - Нийлбэр дээр тоог нэмэхдээ энэхүү тоог нийлбэрийн аль нэг бүрдүүлэгч дээр нэмээд бусад бүрдүүлэгчдийг хөндөхгүй үлдээж болно.
Жишээ нь 15 + 7 нийлбэр дээр 6 -г нэм.
Дүрмийн дагуу нийлбэрийг (15 + 7) + 6 =(15 + 6) + 7 = 21 + 7 =28 эсхүл (15 + 7) + 6 = 15 + (7 + 6) = 15 + 13 =28 гэж тооцож болно.
Дээрх дүрмүүд нь нийлбэрт тоо, нийлбэрийг тоогоор нэмэгдүүлэх үйлдлийг хялбар болгох аргачлал. Арифметикийн нэмэх үйлдэлтэй танилцаж эхлэж буй сурагчид эхлээд нийлбэрийг олоод дараа нь тоон дээрээ нэмэх гэх нь элбэг. Хичээлийн хоёр жишээнд нэг нийлбэр нэг тоо өгөгдсөн байгаа. Ийм жишээг шийдэхдээ сурагчид эхлээд заавал нийлбэрийг тооцоод дараа нь үр дүн дээр тоог нэмэх гээд байдаг. Үүний оронд тоотой энгийн байдлаар нийлбэр үүсгэх аль нэг нэмэгдхүүнийг ашигла гэсэн үг.





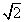
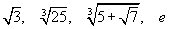
 функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол. тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.